tclean
- tclean(vis, selectdata=True, field='', spw='', timerange='', uvrange='', antenna='', scan='', observation='', intent='', datacolumn='corrected', imagename='', imsize=[100], cell='"1arcsec"', phasecenter='', stokes='I', projection='SIN', startmodel='', specmode='mfs', reffreq='', nchan=-1, start='', width='', outframe='LSRK', veltype='radio', restfreq='', interpolation='linear', perchanweightdensity=True, gridder='standard', facets=1, psfphasecenter='', wprojplanes=1, vptable='', mosweight=True, aterm=True, psterm=False, wbawp=True, conjbeams=False, cfcache='', usepointing=False, computepastep=360.0, rotatepastep=360.0, pointingoffsetsigdev='', pblimit=0.2, normtype='flatnoise', deconvolver='hogbom', scales='', nterms=2, smallscalebias=0.0, fusedthreshold=0.0, largestscale=-1, restoration=True, restoringbeam='', pbcor=False, outlierfile='', weighting='natural', robust=0.5, noise='1.0Jy', npixels=0, uvtaper=[''], niter=0, gain=0.1, threshold=0.0, nsigma=0.0, cycleniter=-1, cyclefactor=1.0, minpsffraction=0.05, maxpsffraction=0.8, interactive=False, nmajor=-1, fullsummary=False, usemask='user', mask='', pbmask=0.0, sidelobethreshold=3.0, noisethreshold=5.0, lownoisethreshold=1.5, negativethreshold=0.0, smoothfactor=1.0, minbeamfrac=0.3, cutthreshold=0.01, growiterations=75, dogrowprune=True, minpercentchange=-1.0, verbose=False, fastnoise=True, restart=True, savemodel='none', calcres=True, calcpsf=True, psfcutoff=0.35, parallel=False)[source]
Radio Interferometric Image Reconstruction
[Description] [Examples] [Development] [Details]
- Parameters
vis ({string, stringVec}) - Name of input visibility file(s)
selectdata (bool=True) - Enable data selection parameters
selectdata = True
field ({string, stringVec}=’’) - field(s) to select
spw ({string, stringVec}=’’) - spw(s)/channels to select
timerange ({string, stringVec}=’’) - Range of time to select from data
uvrange ({string, stringVec}=’’) - Select data within uvrange
antenna ({string, stringVec}=’’) - Select data based on antenna/baseline
scan ({string, stringVec}=’’) - Scan number range
observation ({string, int}=’’) - Observation ID range
intent ({string, stringVec}=’’) - Scan Intent(s)
datacolumn (string=’corrected’) - Data column to image(data,corrected)
imagename ({int, string, stringVec}=’’) - Pre-name of output images
imsize ({int, intVec}=[100]) - Number of pixels
cell ({int, double, intVec, doubleVec, string, stringVec}=‘“1arcsec”’) - Cell size
phasecenter ({int, string}=’’) - Phase center of the image
stokes (string=’I’) - Stokes Planes to make
projection (string=’SIN’) - Coordinate projection
startmodel (string=’’) - Name of starting model image
specmode (string=’mfs’) - Spectral definition mode (mfs,cube,cubedata, cubesource)
specmode = mfs
reffreq (string=’’) - Reference frequency
specmode = cube
nchan (int=-1) - Number of channels in the output image
start (string=’’) - First channel (e.g. start=3,start='1.1GHz',start='15343km/s')
width (string=’’) - Channel width (e.g. width=2,width='0.1MHz',width='10km/s')
outframe (string=’LSRK’) - Spectral reference frame in which to interpret 'start' and 'width'
veltype (string=’radio’) - Velocity type (radio, z, ratio, beta, gamma, optical)
restfreq (stringVec=’’) - List of rest frequencies
interpolation (string=’linear’) - Spectral interpolation (nearest,linear,cubic)
perchanweightdensity (bool=True) - whether to calculate weight density per channel in Briggs style weighting or not
specmode = cubesource
nchan (int=-1) - Number of channels in the output image
start (string=’’) - First channel (e.g. start=3,start='1.1GHz',start='15343km/s')
width (string=’’) - Channel width (e.g. width=2,width='0.1MHz',width='10km/s')
outframe (string=’LSRK’) - Spectral reference frame in which to interpret 'start' and 'width'
veltype (string=’radio’) - Velocity type (radio, z, ratio, beta, gamma, optical)
restfreq (stringVec=’’) - List of rest frequencies
interpolation (string=’linear’) - Spectral interpolation (nearest,linear,cubic)
perchanweightdensity (bool=True) - whether to calculate weight density per channel in Briggs style weighting or not
specmode = cubedata
nchan (int=-1) - Number of channels in the output image
start (string=’’) - First channel (e.g. start=3,start='1.1GHz',start='15343km/s')
width (string=’’) - Channel width (e.g. width=2,width='0.1MHz',width='10km/s')
veltype (string=’radio’) - Velocity type (radio, z, ratio, beta, gamma, optical)
restfreq (stringVec=’’) - List of rest frequencies
interpolation (string=’linear’) - Spectral interpolation (nearest,linear,cubic)
perchanweightdensity (bool=True) - whether to calculate weight density per channel in Briggs style weighting or not
gridder (string=’standard’) - Gridding options (standard, wproject, widefield, mosaic, awproject)
gridder = standard
gridder = widefield
wprojplanes (int=1) - Number of distinct w-values for convolution functions
facets (int=1) - Number of facets on a side
vptable (string=’’) - Name of Voltage Pattern table
pblimit (double=0.2) - PB gain level at which to cut off normalizations
gridder = wproject
wprojplanes (int=1) - Number of distinct w-values for convolution functions
vptable (string=’’) - Name of Voltage Pattern table
pblimit (double=0.2) - PB gain level at which to cut off normalizations
gridder = wprojectft
wprojplanes (int=1) - Number of distinct w-values for convolution functions
vptable (string=’’) - Name of Voltage Pattern table
pblimit (double=0.2) - PB gain level at which to cut off normalizations
gridder = mosaic
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
vptable (string=’’) - Name of Voltage Pattern table
usepointing (bool=False) - The parameter makes the gridder utilize the pointing table phase directions while computing the residual image.
mosweight (bool=True) - Indepently weight each field in a mosaic
pblimit (double=0.2) - PB gain level at which to cut off normalizations
conjbeams (bool=False) - Use conjugate frequency for wideband A-terms
psfphasecenter ({int, string}=’’) - optional direction to calculate psf for mosaic (default is image phasecenter)
gridder = mosaicft
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
vptable (string=’’) - Name of Voltage Pattern table
usepointing (bool=False) - The parameter makes the gridder utilize the pointing table phase directions while computing the residual image.
pblimit (double=0.2) - PB gain level at which to cut off normalizations
conjbeams (bool=False) - Use conjugate frequency for wideband A-terms
psfphasecenter ({int, string}=’’) - optional direction to calculate psf for mosaic (default is image phasecenter)
gridder = ftmosaic
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
vptable (string=’’) - Name of Voltage Pattern table
usepointing (bool=False) - The parameter makes the gridder utilize the pointing table phase directions while computing the residual image.
mosweight (bool=True) - Indepently weight each field in a mosaic
pblimit (double=0.2) - PB gain level at which to cut off normalizations
gridder = imagemosaic
wprojplanes (int=1) - Number of distinct w-values for convolution functions
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
vptable (string=’’) - Name of Voltage Pattern table
pblimit (double=0.2) - PB gain level at which to cut off normalizations
gridder = awproject
wprojplanes (int=1) - Number of distinct w-values for convolution functions
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
psterm (bool=False) - Use prolate spheroidal during gridding
aterm (bool=True) - Use aperture illumination functions during gridding
cfcache (string=’’) - Convolution function cache directory name
computepastep (double=360.0) - Parallactic angle interval after the AIFs are recomputed (deg)
rotatepastep (double=360.0) - Parallactic angle interval after which the nearest AIF is rotated (deg)
pointingoffsetsigdev ({intVec, doubleVec}=’’) - Pointing offset threshold to determine heterogeneity of pointing corrections for the AWProject gridder
wbawp (bool=True) - Use wideband A-terms
mosweight (bool=True) - Indepently weight each field in a mosaic
pblimit (double=0.2) - PB gain level at which to cut off normalizations
conjbeams (bool=False) - Use conjugate frequency for wideband A-terms
usepointing (bool=False) - The parameter makes the gridder utilize the pointing table phase directions while computing the residual image.
gridder = awprojectft
wprojplanes (int=1) - Number of distinct w-values for convolution functions
normtype (string=’flatnoise’) - Normalization type (flatnoise, flatsky,pbsquare)
psterm (bool=False) - Use prolate spheroidal during gridding
aterm (bool=True) - Use aperture illumination functions during gridding
cfcache (string=’’) - Convolution function cache directory name
computepastep (double=360.0) - Parallactic angle interval after the AIFs are recomputed (deg)
rotatepastep (double=360.0) - Parallactic angle interval after which the nearest AIF is rotated (deg)
pointingoffsetsigdev ({intVec, doubleVec}=’’) - Pointing offset threshold to determine heterogeneity of pointing corrections for the AWProject gridder
wbawp (bool=True) - Use wideband A-terms
mosweight (bool=True) - Indepently weight each field in a mosaic
pblimit (double=0.2) - PB gain level at which to cut off normalizations
conjbeams (bool=False) - Use conjugate frequency for wideband A-terms
usepointing (bool=False) - The parameter makes the gridder utilize the pointing table phase directions while computing the residual image.
deconvolver (string=’hogbom’) - Minor cycle algorithm (hogbom,clark,multiscale,mtmfs,mem,clarkstokes,asp)
deconvolver = multiscale
scales ({intVec, doubleVec}=’’) - List of scale sizes (in pixels) for multi-scale algorithms
smallscalebias (double=0.0) - Biases the scale selection when using multi-scale or mtmfs deconvolvers
deconvolver = mtmfs
scales ({intVec, doubleVec}=’’) - List of scale sizes (in pixels) for multi-scale algorithms
nterms (int=2) - Number of Taylor coefficients in the spectral model
smallscalebias (double=0.0) - Biases the scale selection when using multi-scale or mtmfs deconvolvers
deconvolver = asp
fusedthreshold (double=0.0) - Threshold for triggering Hogbom Clean
largestscale (int=-1) - Largest scale allowed for the Asp Clean deconvolver
restoration (bool=True) - Do restoration steps (or not)
restoration = True
restoringbeam ({string, stringVec}=’’) - Restoring beam shape to use. Default is the PSF main lobe
pbcor (bool=False) - Apply PB correction on the output restored image
outlierfile (string=’’) - Name of outlier-field image definitions
weighting (string=’natural’) - Weighting scheme (natural,uniform,briggs, superuniform, radial, briggsabs[experimental], briggsbwtaper[experimental])
weighting = natural
uvtaper (stringVec=[‘’]) - uv-taper on outer baselines in uv-plane
weighting = uniform
uvtaper (stringVec=[‘’]) - uv-taper on outer baselines in uv-plane
weighting = superuniform
uvtaper (stringVec=[‘’]) - uv-taper on outer baselines in uv-plane
weighting = radial
uvtaper (stringVec=[‘’]) - uv-taper on outer baselines in uv-plane
weighting = briggs
weighting = briggsabs
niter (int=0) - Maximum number of iterations
niter != 0
gain (double=0.1) - Loop gain
threshold (double=0.0) - Stopping threshold
nsigma (double=0.0) - Multiplicative factor for rms-based threshold stopping
cycleniter (int=-1) - Maximum number of minor-cycle iterations
cyclefactor (double=1.0) - Scaling on PSF sidelobe level to compute the minor-cycle stopping threshold.
minpsffraction (double=0.05) - PSF fraction that marks the max depth of cleaning in the minor cycle
maxpsffraction (double=0.8) - PSF fraction that marks the minimum depth of cleaning in the minor cycle
interactive (bool=False) - Modify masks and parameters at runtime
nmajor (int=-1) - Maximum number of major cycles to evaluate
fullsummary (bool=False) - Return dictionary with complete convergence history
usemask (string=’user’) - Type of mask(s) for deconvolution: user, pb, or auto-multithresh
usemask = user
usemask = pb
pbmask (double=0.0) - primary beam mask
usemask = auto-multithresh
pbmask (double=0.0) - primary beam mask
sidelobethreshold (double=3.0) - sidelobethreshold * the max sidelobe level * peak residual
noisethreshold (double=5.0) - noisethreshold * rms in residual image + location(median)
lownoisethreshold (double=1.5) - lownoisethreshold * rms in residual image + location(median)
negativethreshold (double=0.0) - negativethreshold * rms in residual image + location(median)
smoothfactor (double=1.0) - smoothing factor in a unit of the beam
minbeamfrac (double=0.3) - minimum beam fraction for pruning
cutthreshold (double=0.01) - threshold to cut the smoothed mask to create a final mask
growiterations (int=75) - number of binary dilation iterations for growing the mask
dogrowprune (bool=True) - Do pruning on the grow mask
minpercentchange (double=-1.0) - minimum percentage change in mask size (per channel plane) to trigger updating of mask by automask
verbose (bool=False) - True: print more automasking information in the logger
fastnoise (bool=True) - True: use the faster (old) noise calculation. False: use the new improved noise calculations
restart (bool=True) - True : Re-use existing images. False : Increment imagename
savemodel (string=’none’) - Options to save model visibilities (none, virtual, modelcolumn)
calcres (bool=True) - Calculate initial residual image
calcpsf (bool=True) - Calculate PSF
calcpsf = True
psfcutoff (double=0.35) - All pixels in the main lobe of the PSF above psfcutoff are used to fit a Gaussian beam (the Clean beam).
parallel (bool=False) - Run major cycles in parallel
- Returns
summary (dict) - convergence history of the run, when interactive=1/0 instead of True/False
Description
Warning
There are Known Issues for tclean
tclean handles continuum images and spectral line cubes, full Stokes polarization imaging, supports outlier fields, contains point-source CLEAN based algorithms as well as options for multi-scale and wideband image reconstruction , widefield imaging correcting for the w-term, full primary-beam imaging and joint mosaic imaging (with heterogeneous array support for ALMA). Parallelization of the major cycle is also available.
The tclean task as based on the CLEAN algorithm , which is the most popular and widely-studied method for reconstructing a model image based on interferometer data. It iteratively removes at each step a fraction of the flux in the brightest pixel in a defined region of the current “dirty” image, and places this in the model image.
Image reconstruction in CASA typically comprises an outer loop of major cycles and an inner loop of minor cycles. The major cycle implements transforms between the data and image domains and the minor cycle operates purely in the image domain. Together, they implement an iterative weighted \(\chi^2\) minimization that solves the measurement equation. Minor cycle algorithms can have their own (different) optimization schemes and the imaging framework and task interface allow for considerable freedom in choosing options separately for each step of the process.
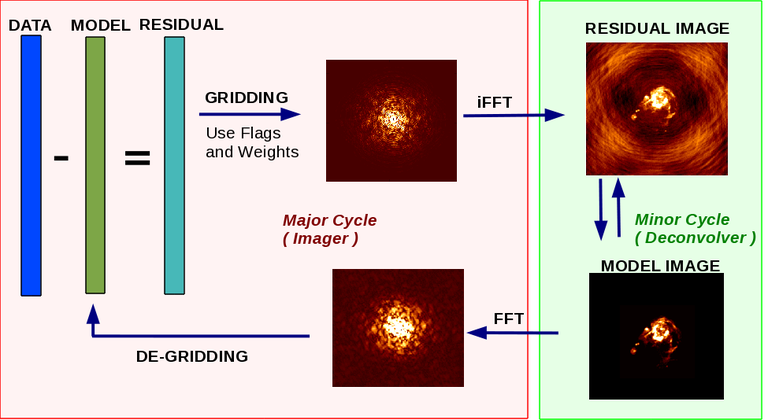
Operating Modes
The tclean task can be configured to perform either full iterative image reconstructions (see synthesis-imaging ) or to run each step separately. Parameters for data selection, image definition, gridding and deconvolution algorithms, restoration and primary beam setup are shared between all operational modes.
The main usage modes of tclean are:
Imaging and Deconvolution Iterations:
Construct the PSF and Dirty image and apply a deconvolution algorithm to reconstruct a Sky model. A series of major and minor cycle iterations are usually performed. The output sky model is then restored and optionally PB-corrected. The Sky model can optionally be saved in the MS during the last major cycle.
Make PSF and PB:
Make only the Point Spread Function and the Primary Beam, along with auxiliary weight images (a single pixel image containing sum-of-weight per plane, and (for mosaic and aprojection) a weight image containing the weighted sum of PB square).
Make a Residual/Dirty Image:
Make a dirty image, or a new residual image using an existing or specified model image. This step requires the presence of the sum-of-weight and weight images (for normalization) constructed during the PSF and PB generation step.
Model Prediction:
Save a sky model in the MeasurementSet for later use in calibration (virtual model or by actual prediction into a model column).
When savemodel=’modelcolumn’ is chosen, the message, “Saving model column” will appear in the logger during the last major cycle. The model will be written to MODEL_DATA column of the main table of the MS for relevant field and spw(s). Similarly, with savemodel=‘virtual’, the message, “Saving virtual model” will appear in the logger. In the case of the virtual model, the model parameters are saved in a keyword of the main table in the MS or in SOURCE subtable. SOURCE subtable is an optional table and if it exists and containing non-zero number of rows, the model parameters are written to SOURCE_MODEL column in the row for the corresponding SOURCE ID. When the virtual model is stored in the keyword of the MS, they are stored with key name such as ‘model_0’. In the case of multiple models exist, say for multiple fields, one can associate particular model key name with a specific field id by looking up the key, ‘definedmodel_field_#’, where # is the field id. Additional information is avaialbe at Virtual Model Visibilities.
To check if model visibility data is present in the MS,
tb.open('xxx.ms') tb.colnames() # will show MODEL_DATA in the the returned column names if MODEL_DATA column exists tb.keywordnames() # if you see, definedmodel_field_{fieldid}, there is a virtual model exists for the field # Also the model parameters (e.g. for 'model_0') can be retrieved by mymodel=tb.getkeyword('model_0') tb.done() # If SOURCE is listed in the keywordnames listing in the above command, and if SOURCE has non-zero rows, virtual model(s) # may exist in SOURCE_MODEL column of SOURCE, # e.g. to get a virutal model for field id=0 (source id=0) tb.open('xxx.ms/SOURCE') mymodel=tb.getcell('SOURCE_MODEL',0) # note that since the model parameter are stored in the record (Python dictionaruy)tb.getcol cannot be used) tb.done()
To check the content of the model data ( either from MODEL_DATA or virutal model generated on the fly),
plotms(vis=‘xxx.ms’, field=‘your_field_that_model_expected_to_be_stored’, spw=.., xaxis=‘uvidist’, yaxis=‘amp’,ydatacolumn=‘model’)
Warning
Please note that tclean may be safely interrupted using a Ctrl-C at all times except when it is in the middle of writing the model data column during a major cycle. To avoid concerns about corrupting your MS by trying to interrupt tclean during a disk write, please run image-reconstruction and model-saving in two separate steps, with model writing turned off during the iterative image reconstruction step. For example:
tclean(vis='xxx.ms', imagename='try',......., niter=20,savemodel='none') tclean(vis='xxx.ms', imagename='try',...., niter=0, savemodel='modelcolumn', calcpsf=False, calcres=False, restoration=False)
This sequence will show a message in the logger that says “Saving Model Column”. Note that while this “predict-only” major cycle is ongoing, Ctrl-C should not be used.
PB-Correction:
Divide out the Primary Beam from the restored Sky image.
pblimit
The pblimit is a parameter used to define the value of the antenna primary beam gain, below which wide-field gridding algorithms such as ‘mosaic’ and ‘awproject’ will not apply normalization (and will therefore set to zero). For gridder=’standard’, ‘wproject’ , ‘widefield’ there is no pb-based normalization during gridding and so the absolute value of this parameter is ignored.
The sign of the pblimit parameter is used for a different purpose. If positive, it defines a T/F pixel mask that is attached to the output residual and restored images. If negative, this T/F pixel mask is not included. For the ‘mosaic’ and ‘awproject’ gridders, the zeros in the regions outside the absolute pblimit level will be visible without the T/F mask, and for other gridders that do not do any pblimit-based normalizations (‘standard’, ‘wproject’, ‘widefield’) those regions will contain valid image pixels.
Please note that this pixel mask is different from the deconvolution mask used to control the region where CLEAN based algorithms will search for source peaks. In order to set a deconvolution mask based on pb level, please use the ‘pbmask’ parameter.
Warning
Certain values of pblimit should be avoided! These values are 1, -1, and 0. Details can be found here.
widebandpbcor
Widebandpbcor is a separate task, and will eventually be implemented as a parameter in tclean. It allows correction of the primary beam as part of wideband imaging. It computes a set of PBs at the specified frequencies, calculates Taylor-coefficient images that represent the PB spectrum, performs a polynomial division to PB-correct the output Taylor-coefficient images from tclean (with nterms>1 and deconvolver=’mtmfs’), and recomputes the spectral index (and curvature) using the PB-corrected Taylor-coefficient images.
Pointing Corrections:
Heterogeneous Pointing Corrections can optionally be applied with the usepointing and pointingoffsetsigdev parameters. These parameters apply corrections based on the pointing errors that are present in the POINTING sub-table. This can improve imaging performance for observations with high wide-band sensitivity, such as is typically observed with the VLA and ALMA telescopes. An overview of pointing corrections is given in the CASA Docs page on Widefield Imaging.
Restoration:
Specify a restoring beam and re-restore the model image.
Auto-masking:
Automatically mask emission during clean; see Masks for Deconvolution for more information.
Output Images
Depending on the operation being run, a subset of the following output images will be written to disk.
imagename = ‘try’
try.psf
Point Spread Function
try.pb
Primary Beam
try.residual
Residual Image (or initial Dirty Image)
try.model
Model Image after deconvolution
try.image
Restored output image
try.image.pbcor
Primary Beam corrected image
try.mask
Deconvolution mask
try.sumwt
A single pixel image containing sum of weights per plane
try.weight
Image of un-normalized sum of PB-square (for mosaics and A-Projection)
try.psf.tt0, try.psf.tt1, try.psf.tt2, try.model.tt0, try.model.tt1, try.residual.tt0, try.residual.tt1, try.image.tt0, try.image.tt1, etc…
Multi-term images representing Taylor coefficients (of polynomials that model the sky spectrum)
try.alpha
Spectral index, for multi-term wideband imagging
try.alpha.error
Estimate of error on spectral index
try.beta
Spectral curvature for multi-term wideband images (if nterms > 2)
try_1.*, try_2.*, try_3.*, etc.
Auto-incremented image names when restart=False
try1_1.*, try1_2.*, try1_3.*, etc.
Auto-incremented image names with multiple fields when restart=False
try.workdirectory
( try.n1.psf, try.n2.psf, try.n3.psf, try.n1.residual, try.n2.residual, try.n3.residual, try.n1.weight, try.n2.weight, try.n3.weight, try.n1.gridwt, try.n2.gridwt, etc… )
Scratch images written within a ‘work directory’ for parallel imaging runs for cube imaging. The reference images are reference-concatenated at the end to produce single output cubes. As of CASA 5.7, continuum imaging no longer produces a try.workdirectory.
Warning
If an image with that name already exists, it will in general be overwritten. Beware using names of existing images however. If the tclean is run using an imagename where <imagename>.residual and <imagename>.model already exist, then tclean will continue starting from these (effectively restarting from the end of the previous tclean). Thus, if multiple runs of tclean are run consecutively with the same imagename, then the cleaning is incremental.
Tip
To organize the output images produced by one or multiple runs of tclean and/or other imaging tasks, a subdirectory can be added to ‘imagename’. All output images will be sent to that directory instead of the current working directory. Example: imagename=’mydir/try’. This is a simple way to group together a set of images (different extensions) corresponding to a same sequence of tclean runs, preventing confusion and conflicts with the potentially long list of other images from related or unrelated tclean runs that used similar ‘imagename’.
Stokes polarization products
It is possible to make polarization images of various Stokes parameters, based on the R/L circular (e.g., VLA) or the X/Y linear (e.g., ALMA) polarization products. When specifying multiple values in the ‘stokes’ parameter, the output image will have planes (along the “polarization” axis) corresponding to the chosen Stokes parameters.
The Stokes parameter is specified as a string of up to four letters, and can indicate stokes parameters themselves, Right/Left hand polarization products, or linear polarization products (X/Y). Examples include:
stokes = 'I' # Intensity only (default) stokes = 'IQU' # Intensity and linear polarization stokes = 'IV' # Intensity and circular polarization stokes = 'IQUV' # All Stokes imaging stokes = 'RR' # Right hand polarization only stokes = 'XXYY' # Both linear polarizations stokes = 'pseudoI' # Intensity only, but including data with one of the parallel polarizations flagged
For imaging the total intensity, the stokes=’I’ option is stricter than the stokes=’pseudoI’ option in the sense that it excludes all correlations for which any correlation is flagged, even though the remaining correlations are valid. On the other hand, the’pseudoI’option allows Stokes I images to include data for which either of the parallel hand data are unflagged. For example, if you have RR and LL dual polarization data and you flagged parts of RR but not LL, stokes=’I’ will ignore both polarizations in the time-stamps where RR are flagged, while stokes=’pseudoI’ will include all unflagged data in the total intensity image. See the CASA Docs pages on Types of Images and Single Dish Imaging (tsdimaging) for more information. It is also possible to split out a polarization product with split and image separately, but you will not be able to combine these part-flagged data in the uv-domain.
Functional Parameter Blocks
The tclean parameters are arranged in the functional blocks described below. More details on the individual parameters and sub-parameters can be found under the Parameters tab at the top of this page.
As a general rule, sub-parameters will appear (and be used) only when a parent parameter has a specific value. This means that for a given set of choices (e.g. deconvolution or gridding algorithm) only parameters that are relevant to that choice will be visible to the user when ” inp() ” is invoked. It is advised that this task interface be used even when constructing tclean scripts that call the task as a python call ” tclean(….) ” to understand which parameters are relevant to the run and which are not.
Data Selection (selectdata)
Selection parameters allow the definition of a subset of the supplied MS (or list of MSs) on which the imaging is to operate. Details can be found on the CASA Docs pages of Visibility Selection.
Image Definition (specmode)
The image coordinate system(s) and shape(s) can be set up to form single images (from a single field or from multiple fields forming a mosaic),or multiple fields. The different modes for imaging include:
‘mfs’: multi-frequency synthesis, i.e., continuum imaging with only one output image channel.
‘cube’: Spectral line imaging with one or more channels. The fixed spectral frame, LSRK, will be used for automatic internal software Doppler tracking so that a spectral line observed over an extended time range will line up appropriately.
‘cubedata’: Spectral line imaging with one or more channels There is no internal software Doppler tracking so a spectral line observed over an extended time range may be smeared out in frequency.
‘cubesource’: Spectral line imaging while tracking moving source (near field or solar system ephemeris objects ). The velocity of the source is accounted and the frequency reported is in the source frame.
Combined use of the parameters ‘specmode’ and ‘gridder’ (see below) allows to specify smaller outlier fields, facetted images, single plane wideband images (with 1 or more Taylor terms to model spectra), 3D spectral cubes with multiple channels, 3D images with multiple Stokes planes, 4D images with frequency channels and Stokes planes. Various combinations of all these options are also supported.
The CASA Docs pages on Image Types provide more details.
Gridding Options (gridder)
Options for convolutional resampling include standard gridding using a prolate spheroidal function, the use of FTs of Fresnel kernels for W-Projection, the use of baseline aperture illumination functions for A-Projection and Mosaicing. These include:
‘standard’: standard gridding using a prolate spheroidal function
‘wproject’: use of FTs of Fresnel kernels to correct for the widefield non-coplanar baseline effect (Cornwell et.al 2008)
‘widefield’: Facetted imaging with or without W-Projection per facet.
‘mosaic’: A-Projection that uses baseline, frequency and time dependent primary beams, without sidelobes, beam rotation or squint correction.
‘awproject’: A-Projection from aperture illumination models with azimuthally asymmetric beams, including beam rotation, squint correction, conjugate frequency beams and W-projection (Bhatnagar et.al, 2008).
Combinations of these options are also available. See the CASA Docs pages on Widefield Imaging for more information.
For mosaicing and AW-projection, the frequency dependence of the primary beam within the data being imaged is included in the calculations and can optionally also be corrected for during gridding. See the CASA Docs page on Wideband Imaging for details.
Deconvolution Options (deconvolver)
All our algorithms follow the Cotton-Schwab CLEAN style of major and minor cycles with the details of the deconvolution algorithm usually contained within the minor cycle and operating in the image domain. Options include:
‘hogbom’: An adapted version of Hogbom Clean (Hogbom, 1974)
‘clark’: An adapted version of Clark Clean (Clark, 1980)
‘clarkstokes’: Clark Clean operating separately per Stokes plane
‘multiscale’: MultiScale Clean (Cornwell, 2008). Scale-sensitive deconvolution algorithm designed for images with complicated spatial structure. It parameterizes the image into a collection of inverted tapered paraboloids.
‘mtmfs’: Multi-term (Multi Scale) Multi-Frequency Synthesis (Rau and Cornwell, 2011). Models the wide-band sky brightness distribution through the use of multi-term Taylor polynomial and wideband primary beam corrections (to be used with nterms>1).
‘mem’: Maximum Entropy Method (Cornwell and Evans, 1985). Note: This algorithm is experimental and not very robust, improvements will be made in the future.
‘asp’: Adaptive Scale Pixel Clean. The Adaptive Scale Pixel (ASP) decomposition algorithm is designed to reconstruct the sky brightness by adaptively determining the optimal scales. The implementation of ASP algorithm is aimed to improve both image resolution and computation efficiency. Note: This algorithm is experimental, please see the Known Issues in CASA Docs.
If as input to tclean the stokes parameter includes polarization planes other than I, then choosing deconvolver=’hogbom’ or ‘clarkstokes’ will clean (search for components) each plane sequentially, while deconvolver =’clark’ will deconvolve jointly.
For more details, see the CASA Docs pages on Deconvolution Algorithms.
Several options for making masks, including automasking, are also provided.
Data Weighting (weighting)
Data weighting during imaging allows for the improvement of the dynamic range and the ability to adjust the synthesized beam associated with the produced image. The weight given to each visibility sample can be adjusted to fit the desired output. There are several reasons to adjust the weighting, including improving sensitivity to extended sources or accounting for noise variation between samples. The user can adjust the weighting by changing the weighting parameter with seven options: ‘natural’, ‘uniform’, ‘briggs’, ‘superuniform’, ‘briggsabs’, ‘briggsbwtaper’, and ‘radial’. Optionally, a UV taper can be applied, and various parameters can be set to further adjust the weight calculations.
The most used options for data weighting are ‘natural’, ‘unform’ and ‘briggs’.
‘Natural’ weighting gives equal weight to all samples, resulting in the lowest noise level and largest (poorest) resolution, with relatively high sidelobe levels.
‘Uniform’ weighting gives a weight inversely proportional to the sampling density function, which minimizes sidelobe levels and provides higher resolution, but at the expense of higher noise levels.
‘Briggs’ weighting provides a compromise between natural and uniform weighting, and often optimizes between angular resolution, noise, and sidelobe levels. The key parameter for briggs weighting is the robust sub-parameter, which takes value between -2.0 (close to uniform weighting) to 2.0 (close to natural). The scaling of Ris such that robust=0 gives a good trade-off between resolution and sensitivity.
In addition to the weighting scheme specified via the ‘weighting’ parameter, additional weights can be applied:
The ‘uvtaper’ parameter applies a Gaussian taper on the weights of the UV data, in addition to the weighting scheme specified via the ‘weighting’ parameter. It is equivalent to smoothing the PSF obtained by other weighting schemes and can be specified either as a Gaussian in uv-space (eg. units of lambda or klambda) or as a Gaussian in the image domain (eg. angular units like arcsec). The effect of uvtaper this is that the clean beam becomes larger, and surface brightness sensitivity increases for extended emission.
The ‘perchanweightdensity’ parameter (for briggs and uniform weighting of cubes) determines whether to calculate the weight density for each channel independently (True) or a common weight density for all of the selected data (False). In general, perchanweightdensity=True (default since CASA 5.5) provides more uniform sensitivity per channel for cubes, but with generally larger PSFs, while perchanweightdensity=False results in smaller psfs for the same robustness value, but the rms noise as a function of channel varies and increases toward the edge channels.
The ‘mosweight’ sub-parameter of the mosaic gridder determines whether to weight each field in a mosaic independently (mosweight = True), or to calculate the weight density from the average uv distribution of all the fields combined (mosweight = False). For ALMA it has been shown that mosweight = True (default since CASA 5.4) may give better results in the presence of poor uv-coverage or non-uniform sensitivity across the mosaic, but the downside is that the major and minor axis of the synthesized beam may be ~10% larger than with mosweight=False, and it may potentially cause memory issues for large VLA mosaics.
More details on data weighting can be found on the Image Algorithm pages of CASA Docs
Iteration Control (niter)
Iterations are controlled by user parameters (gain, niter, etc..) as well as stopping criteria that decide when to exit minor cycle iterations and trigger the next major cycle, and also when to terminate the major-minor loop. These stopping criteria include reaching iteration limits, convergence thresholds, and signs of divergence with appropriate messages displayed in the log. For more details, see the CASA Docs pages on Iteration Control .
Other Options
Handling Large Data and Image Sizes
Parallelization of the major cycle is available for continuum imaging and of both major and minor cycles for cube imaging. In order to run tclean in parallel mode it is necessary to launch CASA with mpicasa, and set the tclean parameter parallel=True. The parallelization of tclean works in the same way if the input is a normal MS or a Multi-MS (MMS), and thus differs from the parallel approach used by other tasks in that it does not require a partitioned MMS file. Details can be found in the CASA Docs chapter on Parallel Processing .
For large image cubes, the gridders can run into memory limits as they loop over all available image planes for each row of data accessed. To prevent this problem, we can grid subsets of channels in sequence with the chanchunks parameter, so that at any given time only part of the image cube needs to be loaded into memory. The chanchunks parameter controls the number of chunks to split the cube into.
User Interaction
Options for user interaction include interactive masking and editing of iteration control parameters. The output log files can also be used to diagnose some problems.
Several convenience features are also available, such as operating on the MS in read-only mode (which does not require write permissions), the ability to restart and continue imaging runs without incuring the unnecessary cost of an initial major cycle or PSF construction and the optional return of a python dictionary that contains the convergence history of the run.
Scripting Controls
Finer control can be achieved using the PySynthesisImager tools to run (for example) only image domain deconvolution or to insert methods for automatic mask generation (for example) in between the existing major/minor cycle loops or to connect external methods or algorithms for either the minor or major cycles.
Tracking moving sources or sources with ephemeris tables
If the phasecenter is a known major solar system object (‘MERCURY’, ‘VENUS’, ‘MARS’, ‘JUPITER’, ‘SATURN’, ‘URANUS’, ‘NEPTUNE’, ‘PLUTO’, ‘SUN’, ‘MOON’) or is an ephemerides table, then that source is tracked and the background sources get smeared (which is useful especially for long observations or multi epoch data). There is a special case, when phasecenter=’TRACKFIELD’, which will use the ephemerides or polynomial phasecenter in the FIELD table of the MeasurementSets as the source center to track. When in tracking mode, the image center will be the direction of the source at the first time in the user selected data. At all other times, the source will be shifted by the amount it has moved in the frame of the image to that initial time. Examples of usage are presented in the tclean examples tab.
Note
When displaying ephemeris images, it is good practice to use relative coordinates to determine the average offset of emission from the ephemeris path over the observation, i.e., axis label properties: world coordinate, relative position. The use of the absolute grid (default) can be misleading since the chosen coordinate frame is associated with the ephemeris path location at an unspecified time, although usually near the beginning of the experimient.
More information can be found in the CASA Docs chapter on Ephemeris Data.
Multiple MSes
For the input visivility data, tclean can accept multiple MSes. The details on conformance checks that are performed on the list of MSes are summarized in the CASA Docs page on Combining Datasets.
History
At the end of a successful tclean run, the history of the output images is updated. For every tclean command a series of entries is recorded, including the task name (tclean), the CASA version used, and every parameter-value pair of the task.
The history is written to all the images associated with the current run, identified by the image base name given in the imagename parameter. This feature searches for all the images with names starting with that basename and followed by a dot-separated extension (imagename.*). In addition it also searches for imagename[INTEGERS]_[INTEGERS].*, to cover auto-incremented image names (see the table of possible image names above).
The image history entries added by tclean can be inspected using the task imhistory (see tasks API), similarly as with the history entries added by other image analysis tasks.
As a lower level interface, the image history can be also inspected and manipulated using CASA tools such as the image analysis tool and the table tool (see tools API). The history entries are written into the ‘logtable’ subtable of the images.
Note
Because history is written into all the images found with the ‘imagename’ prefix and a dot-separated extension, there is a corner case where history entries can be written in images that are not related to the tclean command just executed. For example, if a first tclean command used imagename=’tst.mfs.hogbom’, and a second command uses imagename=’tst.mfs’. This can happen if the tclean commands use the same directory, the imagename string is a shorter version of a previously used imagename, and the longer name is used first and is the shorter name (to be used afterwards) followed by a dot ‘.’ and more characters. This naming scheme produces an ambiguity with the rules used to name output images (imagename + ‘.’ + multiple extensions) and is risky, as it can be very difficult for the user to anticipate all the possible conflicts and confusions with image extensions used by tclean and other imaging tasks.
Processing information
Several parameters related to runtime processing are added to the miscinfo (miscellaneous information) record of the images produced by tclean. These are technical parameters related to processes and memory use:
mpiprocs: integer, number of processes (>1 for parallel runs)
chnchnks: integer, number of sub-cubes or chanchunks into which cubes are partitioned in the major cycles
memavail: float, estimated available memory, as found by tclean at the beginning of the first major cycle.
memreq: float, estimate of memory required, as a function of cube size, number of processors, and a few heuristic scale factors. Expressed in GBs.
These parameters are added to the miscinfo record of the output images by the tclean command that creates them, and represent the runtime processing information of that command.
Similarly as with other parameters included in the miscinfo record, these are exported to FITS images by the exportfits task, if the parameter history is True. The miscinfo record can be inspected using the image tool (see tools API).
The same values are written to the CASA log at the beginning of every major cycle. The memreq estimate should not be interpreted as the amount of memory that tclean is going to use. It is an estimate of memory that would be required to fit all the data in memory, also accounting for the fact that that multiple processes would work on the data simultaneously if running in parallel mode.
The memreq value is used to estimate the required chnchnks or number of sub-cubes into which the data are partitioned in the major cycles. chnchnks is roughly estimated as the result from dividing memreq by memavail. The amount of memory effectively used is kept below the estimated amount of memory available, thanks to the partitioning of the data in sub-cubes and further finer partitioning done in the minor cycles. The memreq estimate grows proportionally to the data dimensions, type of gridder, and number of processes in parallel mode.
- Examples
The following examples, to be expanded, highlight modes and options that the tclean task supports. The examples below are written as scripts that may be copied and pasted to get started with the basic parameters needed for a particular operation. When writing scripts, it is advised that the interactive task interface be used to view lists of sub-parameters that are relevant only to the operations being performed. For example, setting specmode=’cube’ and running inp() will list parameters that are relevant to spectral coordinate definition, or setting niter to a number greater than zero (niter=100) followed by inp() will list iteration control parameters. Note that all runs of tclean need the following parameters: vis, imagename, imsize, and cell. By default, tclean will run with niter=0, making the PSF, a primary beam, the initial dirty (or residual) image and a restored version of the image.
For examples running tclean on ALMA data, see also the ALMA CASA Guide ‘Tclean and ALMA’, which can be found under the General Imaging Tutorial ‘Examples for using the tclean CASA task for ALMA Imaging’.
Imaging and Deconvolution Iterations
Using Hogbom CLEAN on a single MFS image
tclean(vis='test.ms', imagename='try1', imsize=100, cell='10.0arcsec', specmode='mfs', deconvolver='hogbom', gridder='standard', weighting='natural', niter=100 )
Using Multi-scale CLEAN on a Cube Mosaic image
tclean(vis='test.ms', imagename='try1', imsize=100, cell='10.0arcsec',specmode='cube', nchan=10, start='1.0GHz', width='10MHz', deconvolver='multiscale', scales=[0,3,10,30], gridder='mosaic', pblimit=0.1, weighting='natural', niter=100 )
Using W-Projection with Multi-Term MFS wideband imaging
tclean(vis='test.ms', imagename='try1', imsize=100, cell='10.0arcsec', deconvolver='mtmfs', reffreq='1.5GHz', nterms=2, gridder='wproject', wprojplanes=64, weighting='natural', niter=100 )
Using automasking with any type of image
tclean(vis='test.ms', imagename='try1', niter=100, ...., usemask='auto-multithresh')
Scripting using PySynthesisImager
PySynthesisImager (LINK) is a python application built on top of the synthesis tools (LINK). The operations of the tclean task can be replicated using the following python script. Subsets of the script can thus be chosen, and extra external methods can be inserted in between as desired. After each stage, images are saved on disk. Therefore, any modifications done to the images in between steps will be honored.
## (1) Import the python application layer from imagerhelpers.imager_base import PySynthesisImager from imagerhelpers.input_parameters import ImagerParameters ## (2) Set up Input Parameters ## - List all parameters that you need here ## - Defaults will be assumed for unspecified parameters ## - Nearly all parameters are identical to that in the task. ## Please look at the list of parameters under __init__ ## using "help ImagerParameters" paramList = ImagerParameters(msname ='DataTest/point.ms', field='', spw='', imagename='try2', imsize=100, cell='10.0arcsec', specmode='mfs', gridder='standard', weighting='briggs', niter=100, deconvolver='hogbom') ## (3) Construct the PySynthesisImager object, with all input parameters imager = PySynthesisImager(params=paramList) ## (4) Initialize various modules. ## - Pick only the modules you will need later on. For example, to only make ## the PSF, there is no need for the deconvolver or iteration control modules. ## Initialize modules major cycle modules imager.initializeImagers() imager.initializeNormalizers() imager.setWeighting() ## Init minor cycle modules imager.initializeDeconvolvers() imager.initializeIterationControl() ## (5) Make the initial images imager.makePSF() imager.makePB() imager.runMajorCycle() # Make initial dirty / residual image ## (6) Make the initial clean mask imager.hasConverged() imager.updateMask() ## (7) Run the iteration loops while ( not imager.hasConverged() ): imager.runMinorCycle() imager.runMajorCycle() imager.updateMask() ## (8) Finish up retrec=imager.getSummary(); imager.restoreImages() imager.pbcorImages() ## (9) Close tools. imager.deleteTools()
For model prediction (i.e. to only save an input model in preparation for self-calibration, for example), use the following in step (5). The name of the input model is either assumed to be <imagename>.model (or its multi-term equivalent) or should be specified via the startmodel parameter in step (2).
imager.predictModel() # Step (5)
For major cycle parallelization for continuum imaging (specmode=’mfs’), replace steps (1) and (3) with the following
# Step (1) from imagerhelpers.imager_parallel_continuum import PyParallelContSynthesisImager # Step (3) imager = PyParallelContSynthesisImager(params=paramList)
For parallelization of both the major and minor cycles for Cube imaging, replace steps (1) and (3) with the following, and include a virtual concanenation call at the end. (However, note that for parallel Cube imaging, if you would like to replace the minor cycle with your own code (for example), you would have to go one layer deeper. For this, please contact our team for assistance.)
from imagerhelpers.imager_parallel_cube import PyParallelCubeSynthesisImager # Step (1) imager = PyParallelCubeSynthesisImager(params=paramList) # Step (3) imager.concatImages(type='virtualcopy') # Step (8)
Using tclean with ephemerides tables in CASA format
When you have an ephermeris table that covers the whole observation:
tclean(vis=['MS1.ms', 'MS2.ms', 'MS3.ms', 'MS4.ms', 'MS5.ms'], selectdata=True, field="DES_DEEDEE", spw=['17,19,21,23','17,19,21,23','17,19,21,23','17,19,21,23','17,19,21,23'], intent="OBSERVE_TARGET#ON_SOURCE", datacolumn="data", imagename="test_track", imsize=[2000, 2000], cell=['0.037arcsec'], phasecenter="des_deedee_ephem.tab", stokes="I")
You can check whether the ephermeris table is of the format that CASA accepts by using the measures tool me.framecomet function:
me.framecomet('des_deedee.tab')
If this tool accepts the input without complaint, then the same should work in tclean. If the source you are tracking is one of the ten sources for which the CASA measures tool has the ephemerides from the JPL DE200 or DE405, then you can use their names directly:
tclean(vis=['uid___A002_Xbc74ea_X175c.ms', 'uid___A002_Xbc74ea_X1af4.ms', 'uid___A002_Xbc74ea_X1e19.ms', 'uid___A002_Xbc74ea_X20b7.ms'], selectdata=True, field="Jupiter", spw=['17,19,21,23','17,19,21,23','17,19,21,23','17,19,21,23'], intent="OBSERVE_TARGET#ON_SOURCE", datacolumn="corrected", imagename="alltogether", imsize=[700, 700], cell=['0.16arcsec'], phasecenter="JUPITER", stokes="I")
For ALMA data mainly the correlator may have the ephemerides of a moving source already attached to the FIELD tables of the MeasurementSets (as it was used to phase track the source). In such special cases, you can use the keyword “TRACKFIELD” in the phasecenter parameter, and then the internal ephemerides will be used to track the source.
tclean(vis=['MS1.ms', 'MS2.ms', 'MS3.ms', 'MS4.ms', 'MS5.ms'], selectdata=True, field="DES_DEEDEE", spw=['17,19,21,23','17,19,21,23','17,19,21,23','17,19,21,23','17,19,21,23'], intent="OBSERVE_TARGET#ON_SOURCE", datacolumn="data", imagename="test_track", imsize=[2000, 2000], cell=['0.037arcsec'], phasecenter="TRACKFIELD", stokes="I")
- Development
In future releases of CASA6, the tclean task will include an option for MFS and MTMFS deconvolution along with cube major cycles, and GPU gridding options for the VLASS observing program.
- Parameter Details
Detailed descriptions of each function parameter
vis ({string, stringVec})- Name(s) of input visibility file(s)default: none;example: vis=’ngc5921.ms’vis=[‘ngc5921a.ms’,’ngc5921b.ms’]; multiple MSesselectdata (bool=True)- Enable data selection parameters.field ({string, stringVec}='')- Select fields to image or mosaic. Use field id(s) or name(s).[‘go listobs’ to obtain the list id’s or names]default: ‘’= all fieldsIf field string is a non-negative integer, it is assumed tobe a field index otherwise, it is assumed to be afield namefield=’0~2’; field ids 0,1,2field=’0,4,5~7’; field ids 0,4,5,6,7field=’3C286,3C295’; field named 3C286 and 3C295field = ‘3,4C*’; field id 3, all names starting with 4CFor multiple MS input, a list of field strings can be used:field = [‘0~2’,’0~4’]; field ids 0-2 for the first MS and 0-4for the secondfield = ‘0~2’; field ids 0-2 for all input MSesspw ({string, stringVec}='')- Select spectral window/channelsNOTE: channels de-selected here will contain all zeros ifselected by the parameter mode subparameters.default: ‘’=all spectral windows and channelsspw=’0~2,4’; spectral windows 0,1,2,4 (all channels)spw=’0:5~61’; spw 0, channels 5 to 61spw=’<2’; spectral windows less than 2 (i.e. 0,1)spw=’0,10,3:3~45’; spw 0,10 all channels, spw 3,channels 3 to 45.spw=’0~2:2~6’; spw 0,1,2 with channels 2 through 6 in each.For multiple MS input, a list of spw strings can be used:spw=[‘0’,’0~3’]; spw ids 0 for the first MS and 0-3 for the secondspw=’0~3’ spw ids 0-3 for all input MSspw=’3:10~20;50~60’ for multiple channel ranges within spw id 3spw=’3:10~20;50~60,4:0~30’ for different channel ranges for spw ids 3 and 4spw=’0:0~10,1:20~30,2:1;2;3’; spw 0, channels 0-10,spw 1, channels 20-30, and spw 2, channels, 1,2 and 3spw=’1~4;6:15~48’ for channels 15 through 48 for spw ids 1,2,3,4 and 6timerange ({string, stringVec}='')- Range of time to select from datadefault: ‘’ (all); examples,timerange = ‘YYYY/MM/DD/hh:mm:ss~YYYY/MM/DD/hh:mm:ss’Note: if YYYY/MM/DD is missing date defaults to firstday in data settimerange=’09:14:0~09:54:0’ picks 40 min on first daytimerange=’25:00:00~27:30:00’ picks 1 hr to 3 hr30min on NEXT daytimerange=’09:44:00’ pick data within one integrationof timetimerange=’> 10:24:00’ data after this timeFor multiple MS input, a list of timerange strings can beused:timerange=[‘09:14:0~09:54:0’,’> 10:24:00’]timerange=’09:14:0~09:54:0’’; apply the same timerange forall input MSesuvrange ({string, stringVec}='')- Select data within uvrange (default unit is meters)default: ‘’ (all); example:uvrange=’0~1000klambda’; uvrange from 0-1000 kilo-lambdauvrange=’> 4klambda’;uvranges greater than 4 kilo lambdaFor multiple MS input, a list of uvrange strings can beused:uvrange=[‘0~1000klambda’,’100~1000klamda’]uvrange=’0~1000klambda’; apply 0-1000 kilo-lambda for allinput MSesantenna ({string, stringVec}='')- Select data based on antenna/baselinedefault: ‘’ (all)If antenna string is a non-negative integer, it isassumed to be an antenna index, otherwise, it isconsidered an antenna name.antenna=’5&6’; baseline between antenna index 5 andindex 6.antenna=’VA05&VA06’; baseline between VLA antenna 5and 6.antenna=’5&6;7&8’; baselines 5-6 and 7-8antenna=’5’; all baselines with antenna index 5antenna=’05’; all baselines with antenna number 05(VLA old name)antenna=’5,6,9’; all baselines with antennas 5,6,9index numberFor multiple MS input, a list of antenna strings can beused:antenna=[‘5’,’5&6’];antenna=’5’; antenna index 5 for all input MSesantenna=’!DV14’; use all antennas except DV14scan ({string, stringVec}='')- Scan number rangedefault: ‘’ (all)example: scan=’1~5’For multiple MS input, a list of scan strings can be used:scan=[‘0~100’,’10~200’]scan=’0~100; scan ids 0-100 for all input MSesobservation ({string, int}='')- Observation ID rangedefault: ‘’ (all)example: observation=’1~5’intent ({string, stringVec}='')- Scan Intent(s)default: ‘’ (all)example: intent=’TARGET_SOURCE’example: intent=’TARGET_SOURCE1,TARGET_SOURCE2’example: intent=’TARGET_POINTING*’datacolumn (string='corrected')- Data column to image (data or observed, corrected)default:’corrected’( If ‘corrected’ does not exist, it will use ‘data’ instead )imagename ({int, string, stringVec}='')- Pre-name of output imagesexample : imagename=’try’Output images will be (a subset of) :try.psf - Point spread functiontry.residual - Residual imagetry.image - Restored imagetry.model - Model image (contains only flux components)try.sumwt - Single pixel image containing sum-of-weights.(for natural weighting, sensitivity=1/sqrt(sumwt))try.pb - Primary beam model (values depend on the gridder used)Widefield projection algorithms (gridder=mosaic,awproject) willcompute the following images too.try.weight - FT of gridded weights or theun-normalized sum of PB-square (for all pointings)Here, PB = sqrt(weight) normalized to a maximum of 1.0For multi-term wideband imaging, all relevant images above willhave additional .tt0,.tt1, etc suffixes to indicate Taylor terms,plus the following extra output images.try.alpha - spectral indextry.alpha.error - estimate of error on spectral indextry.beta - spectral curvature (if nterms > 2)Tip : Include a directory name in ‘imagename’ for alloutput images to be sent there instead of thecurrent working directory : imagename=’mydir/try’Tip : Restarting an imaging run without changing ‘imagename’implies continuation from the existing model image on disk.- If ‘startmodel’ was initially specified it needs to be set to “”for the restart run (or tclean will exit with an error message).- By default, the residual image and psf will be recomputedbut if no changes were made to relevant parameters betweenthe runs, set calcres=False, calcpsf=False to resume directly fromthe minor cycle without the (unnecessary) first major cycle.To automatically change ‘imagename’ with a numericalincrement, set restart=False (see tclean docs for ‘restart’).Note : All imaging runs will by default produce restored images.For a niter=0 run, this will be redundant and can optionallybe turned off via the ‘restoration=T/F’ parameter.imsize ({int, intVec}=[100])- Number of pixelsexample:imsize = [350,250]imsize = 500 is equivalent to [500,500]To take proper advantage of internal optimized FFT routines, thenumber of pixels must be even and factorizable by 2,3,5 only.To find the nearest optimal imsize to that desired by the user, please use the following tool method:from casatools import synthesisutilssu = synthesisutils()su.getOptimumSize(345)Output : 360cell ({int, double, intVec, doubleVec, string, stringVec}='"1arcsec"')- Cell sizeexample: cell=[‘0.5arcsec,’0.5arcsec’] orcell=[‘1arcmin’, ‘1arcmin’]cell = ‘1arcsec’ is equivalent to [‘1arcsec’,’1arcsec’]phasecenter ({int, string}='')- Phase center of the image (string or field id); if the phasecenter is the name known major solar system object (‘MERCURY’, ‘VENUS’, ‘MARS’, ‘JUPITER’, ‘SATURN’, ‘URANUS’, ‘NEPTUNE’, ‘PLUTO’, ‘SUN’, ‘MOON’) or is an ephemerides table then that source is tracked and the background sources get smeared. There is a special case, when phasecenter=’TRACKFIELD’, which will use the ephemerides or polynomial phasecenter in the FIELD table of the MS’s as the source center to track.Note : If unspecified, tclean will use the phase-center from the first data field of the MS (or list of MSs) selected for imaging.example: phasecenter=6phasecenter=’J2000 19h30m00 -40d00m00’phasecenter=’J2000 292.5deg -40.0deg’phasecenter=’J2000 5.105rad -0.698rad’phasecenter=’ICRS 13:05:27.2780 -049.28.04.458’phasecenter=’myComet_ephem.tab’phasecenter=’MOON’phasecenter=’TRACKFIELD’stokes (string='I')- Stokes Planes to makedefault=’I’; example: stokes=’IQUV’;Options: ‘I’,’Q’,’U’,’V’,’IV’,’QU’,’IQ’,’UV’,’IQUV’,’RR’,’LL’,’XX’,’YY’,’RRLL’,’XXYY’,’pseudoI’Note : Due to current internal code constraints, if any correlation pairis flagged, by default, no data for that row in the MS will be used.So, in an MS with XX,YY, if only YY is flagged, neither aStokes I image nor an XX image can be made from those data points.In such a situation, please split out only the unflagged correlation intoa separate MS.Note : The ‘pseudoI’ option is a partial solution, allowing Stokes I imagingwhen either of the parallel-hand correlations are unflagged.The remaining constraints shall be removed (where logical) in a future release.projection (string='SIN')- Coordinate projectionExamples : SIN, NCPA list of supported (but untested) projections can be found here :startmodel (string='')- Name of starting model imageThe contents of the supplied starting model image will becopied to the imagename.model before the run begins.example : startmodel = ‘singledish.im’For deconvolver=’mtmfs’, one image per Taylor term must be provided.example : startmodel = [‘try.model.tt0’, ‘try.model.tt1’]startmodel = [‘try.model.tt0’] will use a starting model onlyfor the zeroth order term.startmodel = [‘’,’try.model.tt1’] will use a starting model onlyfor the first order term.This starting model can be of a different image shape and size fromwhat is currently being imaged. If so, an image regrid is first triggeredto resample the input image onto the target coordinate system.A common usage is to set this parameter equal to a single dish imageNegative components in the model image will be included as is.[ Note : If an error occurs during image resampling/regridding,please try using task imregrid to resample the starting modelimage onto a CASA image with the target shape andcoordinate system before supplying it via startmodel ]specmode (string='mfs')- Spectral definition mode (mfs,cube,cubedata, cubesource)mode=’mfs’ : Continuum imaging with only one output image channel.(mode=’cont’ can also be used here)mode=’cube’ : Spectral line imaging with one or more channelsParameters start, width,and nchan define the spectralcoordinate system and can be specified either in termsof channel numbers, frequency or velocity in whateverspectral frame is specified in ‘outframe’.All internal and output images are made with outframe as thebase spectral frame. However imaging code internally uses the fixedspectral frame, LSRK for automatic internal softwareDoppler tracking so that a spectral line observed over anextended time range will line up appropriately.Therefore the output images have additional spectral frame conversionlayer in LSRK on the top the base frame.(Note : Even if the input parameters are specified in a frameother than LSRK, the viewer still displays spectralaxis in LSRK by default because of the conversion framelayer mentioned above. The viewer can be used to relabelthe spectral axis in any desired frame - via the spectralreference option under axis label properties in thedata display options window.)mode=’cubedata’ : Spectral line imaging with one or more channelsThere is no internal software Doppler tracking soa spectral line observed over an extended time rangemay be smeared out in frequency. There is strictlyno valid spectral frame with which to associate with theoutput images, thus the image spectral frame willbe labelled “Undefined”.mode=’cubesource’: Spectral line imaging whiletracking moving source (near field or solar systemobjects). The velocity of the source is accountedand the frequency reported is in the source frame.As there is no “SOURCE” frame defined in CASA,the frame in the image will be labelled “REST” (but do note thevelocity of a given line reported may be different from the rest framevelocity if the emission region is moving w.r.t the systemicvelocity frame of the source)reffreq (string='')- Reference frequency of the output image coordinate systemExample : reffreq=’1.5GHz’ as a string with units.By default, it is calculated as the middle of the selected frequency range.For deconvolver=’mtmfs’ the Taylor expansion is also done aboutthis specified reference frequency.nchan (int=-1)- Number of channels in the output imageFor default (=-1), the number of channels will be automatically determinedbased on data selected by ‘spw’ with ‘start’ and ‘width’.It is often easiest to leave nchan at the default value.example: nchan=100start (string='')- First channel (e.g. start=3,start='1.1GHz',start='15343km/s')of output cube images specified by data channel number (integer),velocity (string with a unit), or frequency (string with a unit).Default:’’; The first channel is automatically determined based onthe ‘spw’ channel selection and ‘width’.channels in ‘spw’.Since the integer number in ‘start’ represents the data channel number,when the channel number is used along with the spectral window id selectionin ‘spw’, ‘start’ specified as an integer should be carefully set otherwiseit may result in the blank image channels if the ‘start’ channel (i.e. absolutechannel number) is outside of the channel range specified in ‘spw’.In such a case, ‘start’ can be left as a default (=’’) to ensurematching with the data spectral channel selection.For specmode=’cube’, when velocity or frequency is used it isinterpreted with the frame defined in outframe. [The parameters ofthe desired output cube can be estimated by using the ‘transform’functionality of ‘plotms’]examples: start=’5.0km/s’; 1st channel, 5.0km/s in outframestart=’22.3GHz’; 1st channel, 22.3GHz in outframewidth (string='')- Channel width (e.g. width=2,width='0.1MHz',width='10km/s') of output cube imagesspecified by data channel number (integer), velocity (string with a unit), oror frequency (string with a unit).Default:’’; data channel widthThe sign of width defines the direction of the channels to be incremented.For width specified in velocity or frequency with ‘-’ in front gives image channels indecreasing velocity or frequency, respectively.For specmode=’cube’, when velocity or frequency is used it is interpreted withthe reference frame defined in outframe.examples: width=’2.0km/s’; results in channels with increasing velocitywidth=’-2.0km/s’; results in channels with decreasing velocitywidth=’40kHz’; results in channels with increasing frequencywidth=-2; results in channels averaged of 2 data channels incremented fromhigh to low channel numbersoutframe (string='LSRK')- Spectral reference frame in which to interpret 'start' and 'width'Options: ‘’,’LSRK’,’LSRD’,’BARY’,’GEO’,’TOPO’,’GALACTO’,’LGROUP’,’CMB’example: outframe=’bary’ for Barycentric frameREST – Rest frequencyLSRD – Local Standard of Rest (J2000)– as the dynamical definition (IAU, [9,12,7] km/s in galactic coordinates)LSRK – LSR as a kinematical (radio) definition– 20.0 km/s in direction ra,dec = [270,+30] deg (B1900.0)BARY – Barycentric (J2000)GEO — GeocentricTOPO – TopocentricGALACTO – Galacto centric (with rotation of 220 km/s in direction l,b = [90,0] deg.LGROUP – Local group velocity – 308km/s towards l,b = [105,-7] deg (F. Ghigo)CMB – CMB velocity – 369.5km/s towards l,b = [264.4, 48.4] deg (F. Ghigo)DEFAULT = LSRKveltype (string='radio')- Velocity type (radio, z, ratio, beta, gamma, optical)For start and/or width specified in velocity, specifies the velocity definitionOptions: ‘radio’,’optical’,’z’,’beta’,’gamma’,’optical’NOTE: the viewer always defaults to displaying the ‘radio’ frame,but that can be changed in the position tracking pull down.The different types (with F = f/f0, the frequency ratio), are:Z = (-1 + 1/F)RATIO = (F) *RADIO = (1 - F)OPTICAL == ZBETA = ((1 - F2)/(1 + F2))GAMMA = ((1 + F2)/2F) *RELATIVISTIC == BETA (== v/c)DEFAULT == RADIONote that the ones with an ‘*’ have no real interpretation(although the calculation will proceed) if given as a velocity.restfreq (stringVec='')- List of rest frequencies or a rest frequency in a string.Specify rest frequency to use for output image.*Currently it uses the first rest frequency in the list for translation ofvelocities. The list will be stored in the output images.Default: []; look for the rest frequency stored in the MS, if not available,use center frequency of the selected channelsexamples: restfreq=[‘1.42GHz’]restfreq=’1.42GHz’interpolation (string='linear')- Spectral interpolation (nearest,linear,cubic)Interpolation rules to use when binning data channels onto image channelsand evaluating visibility values at the centers of image channels.Note : ‘linear’ and ‘cubic’ interpolation requires data points on both sides ofeach image frequency. Errors are therefore possible at edge channels, or nearflagged data channels. When image channel width is much larger than the datachannel width there is nothing much to be gained using linear or cubic thusnot worth the extra computation involved.perchanweightdensity (bool=True)- When calculating weight density for Briggsstyle weighting in a cube, this parameterdetermines whether to calculate the weightdensity for each channel independently(the default, True)or a common weight density for all of the selecteddata. This parameter has nomeaning for continuum (specmode=’mfs’) imagingor for natural and radial weighting schemes.For cube imagingperchanweightdensity=True is a recommendedoption that provides more uniformsensitivity per channel for cubes, but withgenerally larger psfs than theperchanweightdensity=False (prior behavior)option. When using Briggs style weight withperchanweightdensity=True, the imaging weightdensity calculations use only the weights ofdata that contribute specifically to thatchannel. On the other hand, whenperchanweightdensity=False, the imagingweight density calculations sum all of theweights from all of the data channelsselected whose (u,v) falls in a given uv cellon the weight density grid. Since theaggregated weights, in any given uv cell,will change depending on the number ofchannels included when imaging, the psfcalculated for a given frequency channel willalso necessarily change, resulting invariability in the psf for a given frequencychannel when perchanweightdensity=False. Ingeneral, perchanweightdensity=False resultsin smaller psfs for the same value ofrobustness compared toperchanweightdensity=True, but the rms noiseas a function of channel varies and increasestoward the edge channels;perchanweightdensity=True provides moreuniform sensitivity per channel forcubes. This may make it harder to findestimates of continuum whenperchanweightdensity=False. If you intend toimage a large cube in many smaller subcubesand subsequently concatenate, it is advisableto use perchanweightdensity=True to avoidsurprisingly varying sensitivity and psfsacross the concatenated cube.gridder (string='standard')- Gridding options (standard, wproject, widefield, mosaic, awproject)The following options choose different gridding convolutionfunctions for the process of convolutional resampling of the measuredvisibilities onto a regular uv-grid prior to an inverse FFT.Model prediction (degridding) also uses these same functions.Several wide-field effects can be accounted for via careful choices ofconvolution functions. Gridding (degridding) runtime will rise inproportion to the support size of these convolution functions (in uv-pixels).standard : Prolate Spheroid with 7x7 uv pixel support size[ This mode can also be invoked using ‘ft’ or ‘gridft’ ]wproject : W-Projection algorithm to correct for the widefieldnon-coplanar baseline effect. [Cornwell et.al 2008]wprojplanes is the number of distinct w-values atwhich to compute and use different gridding convolutionfunctions (see help for wprojplanes).Convolution function support size can rangefrom 5x5 to few 100 x few 100.[ This mode can also be invoked using ‘wprojectft’ ]widefield : Facetted imaging with or without W-Projection per facet.A set of facets x facets subregions of the specified imageare gridded separately using their respective phase centers(to minimize max W). Deconvolution is done on the jointfull size image, using a PSF from the first subregion.wprojplanes=1 : standard prolate spheroid gridder per facet.wprojplanes > 1 : W-Projection gridder per facet.nfacets=1, wprojplanes > 1 : Pure W-Projection and no facettingnfacets=1, wprojplanes=1 : Same as standard,ft,gridftA combination of facetting and W-Projection is relevant only forvery large fields of view. (In our current version of tclean, thiscombination runs only with parallel=False.mosaic : A-Projection with azimuthally symmetric beams withoutsidelobes, beam rotation or squint correction.Gridding convolution functions per visibility are computedfrom FTs of PB models per antenna.This gridder can be run on single fields as well as mosaics.VLA : PB polynomial fit model (Napier and Rots, 1982)EVLA : PB polynomial fit model (Perley, 2015)ALMA : Airy disks for a 10.7m dish (for 12m dishes) and6.25m dish (for 7m dishes) each with 0.75mblockages (Hunter/Brogan 2011). Joint mosaicimaging supports heterogeneous arrays for ALMA.Typical gridding convolution function support sizes arebetween 7 and 50 depending on the desiredaccuracy (given by the uv cell size or image field of view).[ This mode can also be invoked using ‘mosaicft’ or ‘ftmosaic’ ]awproject : A-Projection with azimuthally asymmetric beams andincluding beam rotation, squint correction,conjugate frequency beams and W-projection.[Bhatnagar et.al, 2008]Gridding convolution functions are computed fromaperture illumination models per antenna and optionallycombined with W-Projection kernels and a prolate spheroid.This gridder can be run on single fields as well as mosaics.VLA : Uses ray traced model (VLA and EVLA) including feedleg and subreflector shadows, off-axis feed location(for beam squint and other polarization effects), anda Gaussian fit for the feed beams (Ref: Brisken 2009)ALMA : Similar ray-traced model as above (but the correctnessof its polarization properties remains un-verified).Typical gridding convolution function support sizes arebetween 7 and 50 depending on the desiredaccuracy (given by the uv cell size or image field of view).When combined with W-Projection they can be significantly larger.[ This mode can also be invoked using ‘awprojectft’ ]imagemosaic : (untested implementation)Grid and iFT each pointing separately and combine theimages as a linear mosaic (weighted by a PB model) inthe image domain before a joint minor cycle.VLA/ALMA PB models are same as for gridder=’mosaicft’—— Notes on PB models :(1) Several different sources of PB models are used in the modeslisted above. This is partly for reasons of algorithmic flexibilityand partly due to the current lack of a common beam modelrepository or consensus on what beam models are most appropriate.(2) For ALMA and gridder=’mosaic’, ray-traced (TICRA) beamsare also available via the vpmanager tool.For example, call the following before the tclean run.vp.setpbimage(telescope=”ALMA”,compleximage=’/home/casa/data/trunk/alma/responses/ALMA_0_DV__0_0_360_0_45_90_348.5_373_373_GHz_ticra2007_VP.im’,antnames=[‘DV’+’%02d’%k for k in range(25)])vp.saveastable(‘mypb.tab’)Then, supply vptable=’mypb.tab’ to tclean.( Currently this will work only for non-parallel runs )—— Note on PB masks :In tclean, A-Projection gridders (mosaic and awproject) produce a.pb image and use the ‘pblimit’ subparameter to decide normalizationcutoffs and construct an internal T/F mask in the .pb and .image images.However, this T/F mask cannot directly be used during deconvolution(which needs a 1/0 mask). There are two options for making a pb baseddeconvolution mask.– Run tclean with niter=0 to produce the .pb, construct a 1/0 imagewith the desired threshold (using ia.open(‘newmask.im’);ia.calc(‘iif(“xxx.pb”>0.3,1.0,0.0)’);ia.close() for example),and supply it via the ‘mask’ parameter in a subsequent run(with calcres=F and calcpsf=F to restart directly from the minor cycle).– Run tclean with usemask=’pb’ for it to automatically constructa 1/0 mask from the internal T/F mask from .pb at a fixed 0.2 threshold.—– Making PBs for gridders other than mosaic,awprojectAfter the PSF generation, a PB is constructed using the samemodels used in gridder=’mosaic’ but just evaluated in the imagedomain without consideration to weights.facets (int=1)- Number of facets on a sideA set of (facets x facets) subregions of the specified imageare gridded separately using their respective phase centers(to minimize max W). Deconvolution is done on the jointfull size image, using a PSF from the first subregion/facet.In our current version of tclean, facets>1 may be used onlywith parallel=False.psfphasecenter ({int, string}='')- For mosaic use psf centered on thisoptional direction. You may need to usethis if for example the mosaic does nothave any pointing in the center of theimage. Another reason; as the psf isapproximate for a mosaic, this may helpto deconvolve a non central bright sourcewell and quickly.example:psfphasecenter=6 #center psf on field 6psfphasecenter=’J2000 19h30m00 -40d00m00’psfphasecenter=’J2000 292.5deg -40.0deg’psfphasecenter=’J2000 5.105rad -0.698rad’psfphasecenter=’ICRS 13:05:27.2780 -049.28.04.458’wprojplanes (int=1)- Number of distinct w-values at which to compute and use differentgridding convolution functions for W-ProjectionAn appropriate value of wprojplanes depends on the presence/absenceof a bright source far from the phase center, the desired dynamicrange of an image in the presence of a bright far out source,the maximum w-value in the measurements, and the desired trade offbetween accuracy and computing cost.As a (rough) guide, VLA L-Band D-config may require avalue of 128 for a source 30arcmin away from the phasecenter. A-config may require 1024 or more. To converge to anappropriate value, try starting with 128 and then increasingit if artifacts persist. W-term artifacts (for the VLA) typically looklike arc-shaped smears in a synthesis image or a shift in sourceposition between images made at different times. These artifactsare more pronounced the further the source is from the phase center.There is no harm in simply always choosing a large value (say, 1024)but there will be a significant performance cost to doing so, especiallyfor gridder=’awproject’ where it is combined with A-Projection.wprojplanes=-1 is an option for gridder=’widefield’ or ‘wproject’in which the number of planes is automatically computed.vptable (string='')- VP table saved via the vpmanagervptable=”” : Choose default beams for different telescopesALMA : Airy disksEVLA : old VLA models.Other primary beam models can be chosen via the vpmanager tool.Step 1 : Set up the vpmanager tool and save its state in a tablevp.setpbpoly(telescope=’EVLA’, coeff=[1.0, -1.529e-3, 8.69e-7, -1.88e-10])vp.saveastable(‘myvp.tab’)Step 2 : Supply the name of that table in tclean.tclean(….., vptable=’myvp.tab’,….)Please see the documentation for the vpmanager for more details on how tochoose different beam models. Work is in progress to update the defaultsfor EVLA and ALMA.Note : AWProjection currently does not use this mechanism to choosebeam models. It instead uses ray-traced beams computed fromparameterized aperture illumination functions, which are notavailable via the vpmanager. So, gridder=’awproject’ does not allowthe user to set this parameter.mosweight (bool=True)- When doing Brigg’s style weighting (including uniform) to perform the weight density calculation for each field indepedently if True. If False the weight density is calculated from the average uv distribution of all the fields.aterm (bool=True)- Use aperture illumination functions during griddingThis parameter turns on the A-term of the AW-Projection gridder.Gridding convolution functions are constructed from aperture illuminationfunction models of each antenna.psterm (bool=False)- Include the Prolate Spheroidal (PS) funtion as the anti-aliasingoperator in the gridding convolution functions used for gridding.Setting this parameter to true is necessary when aterm is set tofalse. It can be set to false when aterm is set to true, thoughwith this setting effects of aliasing may be there in the image,particularly near the edges.When set to true, the .pb images will contain the fourier transformof the of the PS funtion. The table below enumarates the functionaleffects of the psterm, aterm and wprojplanes settings. PB referes tothe Primary Beam and FT() refers to the Fourier transform operation.Operation aterm psterm wprojplanes Contents of the .pb image———————————————————————-AW-Projection True True >1 FT(PS) x PBFalse PBA-Projection True True 1 FT(PS) x PBFalse PBW-Projection False True >1 FT(PS)Standard False True 1 FT(PS)wbawp (bool=True)- Use frequency dependent A-termsScale aperture illumination functions appropriately with frequencywhen gridding and combining data from multiple channels.conjbeams (bool=False)- Use conjugate frequency for wideband A-termsWhile gridding data from one frequency channel, choose a convolutionfunction from a ‘conjugate’ frequency such that the resulting baselineprimary beam is approximately constant across frequency. For a system inwhich the primary beam scales with frequency, this step will eliminateinstrumental spectral structure from the measured data and leave only thesky spectrum for the minor cycle to model and reconstruct [Bhatnagar et al., ApJ, 2013].As a rough guideline for when this is relevant, a source at the half powerpoint of the PB at the center frequency will see an artificial spectralindex of -1.4 due to the frequency dependence of the PB [Sault and Wieringa, 1994].If left uncorrected during gridding, this spectral structure must be modeledin the minor cycle (using the mtmfs algorithm) to avoid dynamic range limits(of a few hundred for a 2:1 bandwidth).This works for specmode=’mfs’ and its value is ignored for cubescfcache (string='')- Convolution function cache directory nameName of a directory in which to store gridding convolution functions.This cache is filled at the beginning of an imaging run. This step can be timeconsuming but the cache can be reused across multiple imaging runs thatuse the same image parameters (cell size, image size , spectral dataselections, wprojplanes, wbawp, psterm, aterm). The effect of the wbawp,psterm and aterm settings is frozen-in in the cfcache. Using an existing cfcachemade with a different setting of these parameters will not reflect the currentsettings.In a parallel execution, the construction of the cfcache is also parallelizedand the time to compute scales close to linearly with the number of computecores used. With the re-computation of Convolution Functions (CF) due to PArotation turned-off (the computepastep parameter), the total number of in thecfcache can be computed as [No. of wprojplanes x No. of selected spectral windows x 4]By default, cfcache = imagename + ‘.cf’usepointing (bool=False)- The usepointing flag informs the gridder that it should utilize the pointing tableto use the correct direction in which the antenna is pointing with respect to the pointing phasecenter.computepastep (double=360.0)- Parallactic angle interval after the AIFs are recomputed (deg)This parameter controls the accuracy of the aperture illumination functionused with AProjection for alt-az mount dishes where the AIF rotates on thesky as the synthesis image is built up. Once the PA in the data changes bythe given interval, AIFs are re-computed at the new PA.A value of 360.0 deg (the default) implies no re-computation due to PA rotation.AIFs are computed for the PA value of the first valid data received and used forall of the data.rotatepastep (double=360.0)- Parallactic angle interval after which the nearest AIF is rotated (deg)Instead of recomputing the AIF for every timestep’s parallactic angle,the nearest existing AIF is used and rotatedafter the PA changed by rotatepastep value.A value of 360.0 deg (the default) disables rotation of the AIF.For example, computepastep=360.0 and rotatepastep=5.0 will computethe AIFs at only the starting parallactic angle and all other timesteps willuse a rotated version of that AIF at the nearest 5.0 degree point.pointingoffsetsigdev ({intVec, doubleVec}='')- Corrections for heterogenous and time-dependent pointingoffsets via AWProjection are controlled by this parameter.It is a vector of 2 ints or doubles each of which is interpretedin units of arcsec. Based on the first threshold, a clusteringalgorithm is applied to entries from the POINTING subtableof the MS to determine how distinct antenna groups for whichthe pointing offset must be computed separately. The secondnumber controls how much a pointing change across time canbe ignored and after which an antenna rebinning is required.Note : The default value of this parameter is [], due a programmatic constraint.If run with this value, it will internally pick [600,600] and exercise theoption of using large tolerances (10arcmin) on both axes. Please choosea setting explicitly for runs that need to use this parameter.Note : This option is available only for gridder=’awproject’ and usepointing=True andand has been validated primarily with VLASS on-the-fly mosaic datawhere POINTING subtables have been modified after the data are recorded.Examples of parameter usage :[100.0,100.0] : Pointing offsets of 100 arcsec or less are consideredsmall enough to be ignored. Using large values for bothindicates a homogeneous array.[10.0, 100.0] : Based on entries in the POINTING subtable, antennasare grouped into clusters based on a 10arcsec bin size.All antennas in a bin are given a pointing offset calculatedas the average of the offsets of all antennas in the bin.On the time axis, offset changes upto 100 arcsec will be ignored.[10.0,10.0] : Calculate separate pointing offsets for each antenna group(with a 10 arcsec bin size). As a function of time, recalculatethe antenna binning if the POINTING table entries change bymore than 10 arcsec w.r.to the previously computed binning.[1.0, 1.0] : Tight tolerances will imply a fully heterogenous situation whereeach antenna gets its own pointing offset. Also, time-dependentoffset changes greater than 1 arcsec will trigger recomputes ofthe phase gradients. This is the most general situation and is alsothe most expensive option as it constructs and uses separatephase gradients for all baselines and timesteps.For VLASS 1.1 data with two kinds of pointing offsets, the recommendedsetting is [ 30.0, 30.0 ].For VLASS 1.2 data with only the time-dependent pointing offsets, therecommended setting is [ 300.0, 30.0 ] to turn off the antenna groupingbut to retain the time dependent corrections required from one timestepto the next.pblimit (double=0.2)- PB gain level at which to cut off normalizationsDivisions by .pb during normalizations have a cut off at a .pb gainlevel given by pblimit. Outside this limit, image values are set to zero.Additionally, by default, an internal T/F mask is applied to the .pb, .image and.residual images to mask out (T) all invalid pixels outside the pblimit area.Note : This internal T/F mask cannot be used as a deconvolution mask.To do so, please follow the steps listed above in the Notes for the‘gridder’ parameter.Note : To prevent the internal T/F mask from appearing in anything otherthan the .pb and .image.pbcor images, ‘pblimit’ can be set to anegative number.The absolute value will still be used as a valid ‘pblimit’ for normalizationpurposes. So, for example, pick pblimit=-0.1 (and not pblimit=-1).A tclean restart using existing output images on disk that alreadyhave this T/F mask in the .residual and .image but only pblimit setto a negative value, will remove this mask after the next major cycle.Note : An existing internal T/F mask may be removed from an image asfollows (without needing to re-run tclean itself).ia.open(‘test.image’);ia.maskhandler(op=’set’, name=’’);ia.done()normtype (string='flatnoise')- Normalization type (flatnoise, flatsky, pbsquare)Gridded (and FT’d) images represent the PB-weighted sky image.Qualitatively it can be approximated as two instances of the PBapplied to the sky image (one naturally present in the dataand one introduced during gridding via the convolution functions).xxx.weight : Weight image approximately equal to sum ( square ( pb ) )xxx.pb : Primary beam calculated as sqrt ( xxx.weight )normtype=’flatnoise’ : Divide the raw image by sqrt(.weight) so thatthe input to the minor cycle represents theproduct of the sky and PB. The noise is ‘flat’across the region covered by each PB.normtype=’flatsky’ : Divide the raw image by .weight so that the inputto the minor cycle represents only the sky.The noise is higher in the outer regions of theprimary beam where the sensitivity is low.normtype=’pbsquare’ : No normalization after gridding and FFT.The minor cycle sees the sky times pb squaredeconvolver (string='hogbom')- Name of minor cycle algorithm (hogbom,clark,multiscale,mtmfs,mem,clarkstokes,asp)Each of the following algorithms operate on residual images and psfsfrom the gridder and produce output model and restored images.Minor cycles stop and a major cycle is triggered when cyclethresholdor cycleniter are reached. For all methods, components are picked fromthe entire extent of the image or (if specified) within a mask.hogbom : An adapted version of Hogbom Clean [Hogbom, 1974]- Find the location of the peak residual- Add this delta function component to the model image- Subtract a scaled and shifted PSF of the same size as the imagefrom regions of the residual image where the two overlap.- Repeatclark : An adapted version of Clark Clean [Clark, 1980]- Find the location of max(I^2+Q^2+U^2+V^2)- Add delta functions to each stokes plane of the model image- Subtract a scaled and shifted PSF within a small patch sizefrom regions of the residual image where the two overlap.- After several iterations trigger a Clark major cycle to subtractcomponents from the visibility domain, but without de-gridding.- Repeat( Note : ‘clark’ maps to imagermode=’’ in the old clean task.‘clark_exp’ is another implementation that maps toimagermode=’mosaic’ or ‘csclean’ in the old clean taskbut the behavior is not identical. For now, pleaseuse deconvolver=’hogbom’ if you encounter problems. )clarkstokes : Clark Clean operating separately per Stokes plane(Note : ‘clarkstokes_exp’ is an alternate version. See above.)multiscale : MultiScale Clean [Cornwell, 2008]- Smooth the residual image to multiple scale sizes- Find the location and scale at which the peak occurs- Add this multiscale component to the model image- Subtract a scaled,smoothed,shifted PSF (within a smallpatch size per scale) from all residual images- Repeat from step 2mtmfs : Multi-term (Multi Scale) Multi-Frequency Synthesis [Rau and Cornwell, 2011]- Smooth each Taylor residual image to multiple scale sizes- Solve a NTxNT system of equations per scale size to computeTaylor coefficients for components at all locations- Compute gradient chi-square and pick the Taylor coefficientsand scale size at the location with maximum reduction inchi-square- Add multi-scale components to each Taylor-coefficientmodel image- Subtract scaled,smoothed,shifted PSF (within a small patch sizeper scale) from all smoothed Taylor residual images- Repeat from step 2mem : Maximum Entropy Method [Cornwell and Evans, 1985]- Iteratively solve for values at all individual pixels via theMEM method. It minimizes an objective function ofchi-square plus entropy (here, a measure of differencebetween the current model and a flat prior model).(Note : This MEM implementation is not very robust.Improvements will be made in the future.)asp : Adaptive Scale Pixel algorithm [Bhatnagar and Cornwell, 2004]- Define a set of initial scales defined as 0, W, 2W 4W and 8Wwhere W is a 2D Gaussian fitting width to the PSF- Smooth the residual image by a Gaussian beam at initial scales- Search for the global peak (F) among these smoothed residual images- form an active Aspen set: amplitude(F), amplitude location(x,y)- Optimize the Aspen set by minimizing the objective function RI-Aspen*PSF,where RI is the residual image and * is the convulition operation.- Compute the model image and update the residual image- Repeat from step 2(Note : This is an experimental version of the ASP algorithm.)scales ({intVec, doubleVec}='')- List of scale sizes (in pixels) for multi-scale and mtmfs algorithms.–> scales=[0,6,20]This set of scale sizes should represent the sizes(diameters in units of number of pixels)of dominant features in the image being reconstructed.The smallest scale size is recommended to be 0 (point source),the second the size of the synthesized beam and the third 3-5times the synthesized beam, etc. For example, if the synthesizedbeam is 10” FWHM and cell=2”,try scales = [0,5,15].For numerical stability, the largest scale must besmaller than the image (or mask) size and smaller than orcomparable to the scale corresponding to the lowest measuredspatial frequency (as a scale size much larger than what theinstrument is sensitive to is unconstrained by the data makingit harder to recovery from errors during the minor cycle).nterms (int=2)- Number of Taylor coefficients in the spectral model- nterms=1 : Assume flat spectrum source- nterms=2 : Spectrum is a straight line with a slope- nterms=N : A polynomial of order N-1From a Taylor expansion of the expression of a power law, thespectral index is derived as alpha = taylorcoeff_1 / taylorcoeff_0Spectral curvature is similarly derived when possible.The optimal number of Taylor terms depends on the availablesignal to noise ratio, bandwidth ratio, and spectral shape of thesource as seen by the telescope (sky spectrum x PB spectrum).nterms=2 is a good starting point for wideband EVLA imagingand the lower frequency bands of ALMA (when fractional bandwidthis greater than 10%) and if there is at least one bright source forwhich a dynamic range of greater than few 100 is desired.Spectral artifacts for the VLA often look like spokes radiating out froma bright source (i.e. in the image made with standard mfs imaging).If increasing the number of terms does not eliminate these artifacts,check the data for inadequate bandpass calibration. If the source is awayfrom the pointing center, consider including wide-field corrections too.(Note : In addition to output Taylor coefficient images .tt0,.tt1,etcimages of spectral index (.alpha), an estimate of error onspectral index (.alpha.error) and spectral curvature (.beta,if nterms is greater than 2) are produced.- These alpha, alpha.error and beta images containinternal T/F masks based on a threshold computedas peakresidual/10. Additional masking based on.alpha/.alpha.error may be desirable.- .alpha.error is a purely empirical estimate derivedfrom the propagation of error during the division oftwo noisy numbers (alpha = xx.tt1/xx.tt0) where the‘error’ on tt1 and tt0 are simply the values picked fromthe corresponding residual images. The absolute valueof the error is not always accurate and it is best to interpretthe errors across the image only in a relative sense.)smallscalebias (double=0.0)- A numerical control to bias the scales when using multi-scale or mtmfs algorithms.The peak from each scale’s smoothed residual ismultiplied by ( 1 - smallscalebias * scale/maxscale )to increase or decrease the amplitude relative to other scales,before the scale with the largest peak is chosen.Smallscalebias can be varied between -1.0 and 1.0.A score of 0.0 gives all scales equal weight (default).A score larger than 0.0 will bias the solution towards smaller scales.A score smaller than 0.0 will bias the solution towards larger scales.The effect of smallscalebias is more pronounced when using multi-scale relative to mtmfs.fusedthreshold (double=0.0)- Threshold for triggering Hogbom Clean (number in units of Jy)fusedthreshold = 0.0001 : 0.1 mJyThis is a subparameter of the Asp Clean deconvolver. When peak residualis lower than the threshold, Asp Clean is “switched to Hogbom Clean” (i.e. only use the 0 scale for cleaning) forthe following number of iterations until it switches back to Asp Clean.NumberIterationsInHogbom = 50 + 2 * (exp(0.05 * NthHogbom) - 1), where NthHogbom is the number of times Hogbom Clean has been triggered.When the Asp Clean detects it is approaching convergence, it uses only the 0 scale for the following number of iterations for better computational efficiency.NumberIterationsInHogbom = 500 + 2 * (exp(0.05 * NthHogbom) - 1)Set ‘fusedthreshold = -1’ to make the Asp Clean deconvolver never “switch” to Hogbom Clean.largestscale (int=-1)- Largest scale (in pixels) allowed for the initial guess for the Asp Clean deconvolver.largestscale = 100The default initial scale sizes used by Asp Clean is [0, w, 2w, 4w, 8w],where w is the PSF width. The default largestscale is -1 which indicatesusers accept these initial scales. If largestscale is set, the initial scaleswould be [0, w, … up to the largestscale]. This is only an initial guess,and actual fitted scale sizes may evolve from these initial values.It is recommended not to set largestscale unless Asp Clean picks a largescale that has no constraints from the data (the UV hole issue).restoration (bool=True)- Restore the model image.Construct a restored image : imagename.image by convolving the modelimage with a clean beam and adding the residual image to the result.If a restoringbeam is specified, the residual image is alsosmoothed to that target resolution before adding it in.If a .model does not exist, it will make an empty one and createthe restored image from the residuals ( with additional smoothing if needed ).With algorithm=’mtmfs’, this will construct Taylor coefficient maps fromthe residuals and compute .alpha and .alpha.error.restoringbeam ({string, stringVec}='')- Restoring beam shape/size to use.- restoringbeam=’’ or [‘’]A Gaussian fitted to the PSF main lobe (separately per image plane).- restoringbeam=’10.0arcsec’Use a circular Gaussian of this width for all planes- restoringbeam=[‘8.0arcsec’,’10.0arcsec’,’45deg’]Use this elliptical Gaussian for all planes- restoringbeam=’common’Automatically estimate a common beam shape/size appropriate forall planes.Note : For any restoring beam different from the native resolutionthe model image is convolved with the beam and added toresiduals that have been convolved to the same target resolution.pbcor (bool=False)- Apply PB correction on the output restored imageA new image with extension .image.pbcor will be created fromthe evaluation of .image / .pb for all pixels above the specified pblimit.Note : Stand-alone PB-correction can be triggered by re-runningtclean with the appropriate imagename and withniter=0, calcpsf=False, calcres=False, pbcor=True, vptable=’vp.tab’( where vp.tab is the name of the vpmanager file.See the inline help for the ‘vptable’ parameter )Note : Multi-term PB correction that includes a correction for thespectral index of the PB has not been enabled for the 4.7 release.Please use the widebandpbcor task instead.( Wideband PB corrections are required when the amplitude of thebrightest source is known accurately enough to be sensitiveto the difference in the PB gain between the upper and lowerend of the band at its location. As a guideline, the artificial spectralindex due to the PB is -1.4 at the 0.5 gain level and less than -0.2at the 0.9 gain level at the middle frequency )outlierfile (string='')- Name of outlier-field image definitionsA text file containing sets of parameter=value pairs,one set per outlier field.Example : outlierfile=’outs.txt’Contents of outs.txt :imagename=tst1nchan=1imsize=[80,80]cell=[8.0arcsec,8.0arcsec]phasecenter=J2000 19:58:40.895 +40.55.58.543mask=circle[[40pix,40pix],10pix]imagename=tst2nchan=1imsize=[100,100]cell=[8.0arcsec,8.0arcsec]phasecenter=J2000 19:58:40.895 +40.56.00.000mask=circle[[60pix,60pix],20pix]The following parameters are currently allowed to be different betweenthe main field and the outlier fields (i.e. they will be recognized if foundin the outlier text file). If a parameter is not listed, the value is picked fromwhat is defined in the main task input.imagename, imsize, cell, phasecenter, startmodel, maskspecmode, nchan, start, width, nterms, reffreq,gridder, deconvolver, wprojplanesNote : ‘specmode’ is an option, so combinations of mfs and cubefor different image fields, for example, are supported.‘deconvolver’ and ‘gridder’ are also options that allow differentimaging or deconvolution algorithm per image field.For example, multiscale with wprojection and 16 w-term planeson the main field and mtmfs with nterms=3 and wprojectionwith 64 planes on a bright outlier source for which the frequencydependence of the primary beam produces a strong effect thatmust be modeled. The traditional alternative to this approach isto first image the outlier, subtract it out of the data (uvsub) andthen image the main field.Note : If you encounter a use-case where some other parameter needsto be allowed in the outlier file (and it is logical to do so), pleasesend us feedback. The above is an initial list.weighting (string='natural')- Weighting scheme (natural,uniform,briggs,superuniform,radial, briggsabs, briggsbwtaper)During gridding of the dirty or residual image, each visibility value ismultiplied by a weight before it is accumulated on the uv-grid.The PSF’s uv-grid is generated by gridding only the weights (weightgrid).weighting=’natural’ : Gridding weights are identical to the data weightsfrom the MS. For visibilities with similar data weights,the weightgrid will follow the sample densitypattern on the uv-plane. This weighting schemeprovides the maximum imaging sensitivity at theexpense of a possibly fat PSF with high sidelobes.It is most appropriate for detection experimentswhere sensitivity is most important.weighting=’uniform’ : Gridding weights per visibility data point are theoriginal data weights divided by the total weight ofall data points that map to the same uv grid cell :‘ data_weight / total_wt_per_cell ‘.The weightgrid is as close to flat as possible resultingin a PSF with a narrow main lobe and suppressedsidelobes. However, since heavily sampled areas ofthe uv-plane get down-weighted, the imagingsensitivity is not as high as with natural weighting.It is most appropriate for imaging experiments wherea well behaved PSF can help the reconstruction.weighting=’briggs’ : Gridding weights per visibility data point are given by‘data_weight / ( A * total_wt_per_cell + B ) ‘ whereA and B vary according to the ‘robust’ parameter.robust = -2.0 maps to A=1,B=0 or uniform weighting.robust = +2.0 maps to natural weighting.(robust=0.5 is equivalent to robust=0.0 in AIPS IMAGR.)Robust/Briggs weighting generates a PSF that canvary smoothly between ‘natural’ and ‘uniform’ andallow customized trade-offs between PSF shape andimaging sensitivity.weighting=’briggsabs’ : Experimental option.Same as Briggs except the formula is different A=robust*robust and B is dependent on thenoise per visibility estimated. Giving noise=’0Jy’is a not a reasonable option.In this mode (or formula) robust valuesfrom -2.0 to 0.0 only make sense (2.0 and-2.0 will get the same weighting)weighting=’superuniform’ : This is similar to uniform weighting except thatthe total_wt_per_cell is replaced by thetotal_wt_within_NxN_cells around the uv cell ofinterest. N=7 is the default (when theparameter ‘npixels’ is set to 0 with ‘superuniform’)This method tends to give a PSF with innersidelobes that are suppressed as in uniformweighting but with far-out sidelobes closer tonatural weighting. The peak sensitivity is alsocloser to natural weighting.weighting=’radial’ : Gridding weights are given by ‘ data_weight * uvdistance ‘This method approximately minimizes rms sidelobesfor an east-west synthesis array.weighting=’briggsbwtaper’ : A modified version of Briggs weighting for cubes where an inverse uv taper,which is proportional to the fractional bandwidth of the entire cube,is applied per channel. The objective is to modify cube (perchanweightdensity = True)imaging weights to have a similar density to that of the continuum imaging weights.This is currently an experimental weighting scheme being developed for ALMA.For more details on weighting please see Chapter3of Dan Briggs’ thesis (http://www.aoc.nrao.edu/dissertations/dbriggs)robust (double=0.5)- Robustness parameter for Briggs weighting.robust = -2.0 maps to uniform weighting.robust = +2.0 maps to natural weighting.(robust=0.5 is equivalent to robust=0.0 in AIPS IMAGR.)noise (variant='1.0Jy')- noise parameter for briggs abs mode weightingnpixels (int=0)- Number of pixels to determine uv-cell size for super-uniform weighting(0 defaults to -/+ 3 pixels)npixels – uv-box used for weight calculationa box going from -npixel/2 to +npixel/2 on each sidearound a point is used to calculate weight density.npixels=2 goes from -1 to +1 and covers 3 pixels on a side.npixels=0 implies a single pixel, which does not make sense forsuperuniform weighting. Therefore, for ‘superuniform’weighting, if npixels=0 it will be forced to 6 (or a boxof -3pixels to +3pixels) to cover 7 pixels on a side.uvtaper (stringVec=[''])- uv-taper on outer baselines in uv-planeApply a Gaussian taper in addition to the weighting scheme specifiedvia the ‘weighting’ parameter. Higher spatial frequencies are weighteddown relative to lower spatial frequencies to suppress artifactsarising from poorly sampled areas of the uv-plane. It is equivalent tosmoothing the PSF obtained by other weighting schemes and can bespecified either as the HWHM of a Gaussian in uv-space (eg. units of lambda)or as the FWHM of a Gaussian in the image domain (eg. angular units like arcsec).uvtaper = [bmaj, bmin, bpa]Note : FWHM_uv_lambda = (4 log2) / ( pi * FWHM_lm_radians )A FWHM_lm of 100.000 arcsec maps to a HWHM_uv of 910.18 lambdaA FWHM_lm of 1 arcsec maps to a HWHM_uv of 91 klambdadefault: uvtaper=[]; no Gaussian taper appliedexample: uvtaper=[‘5klambda’] circular taper of HWHM=5 kilo-lambdauvtaper=[‘5klambda’,’3klambda’,’45.0deg’] uv-domain HWHMuvtaper=[‘50arcsec’,’30arcsec’,’30.0deg’] : image domain FWHMuvtaper=[‘10arcsec’] : image domain FWHMuvtaper=[‘300.0’] default units are lambda in aperture planeniter (int=0)- Maximum number of iterationsA stopping criterion based on total iteration count.Currently the parameter type is defined as an integer therefore the integer valuelarger than 2147483647 will not be set properly as it causes an overflow.Iterations are typically defined as the selecting one flux componentand partially subtracting it out from the residual image.niter=0 : Do only the initial major cycle (make dirty image, psf, pb, etc)niter larger than zero : Run major and minor cycles.Note : Global stopping criteria vs major-cycle triggersIn addition to global stopping criteria, the following rules areused to determine when to terminate a set of minor cycle iterationsand trigger major cycles [derived from Cotton-Schwab Clean, 1984]‘cycleniter’ : controls the maximum number of iterations per imageplane before triggering a major cycle.‘cyclethreshold’ : Automatically computed threshold related to themax sidelobe level of the PSF and peak residual.Divergence, detected as an increase of 10% in peak residual from theminimum so far (during minor cycle iterations)The first criterion to be satisfied takes precedence.Note : Iteration counts for cubes or multi-field images :For images with multiple planes (or image fields) on which thedeconvolver operates in sequence, iterations are counted acrossall planes (or image fields). The iteration count is compared with‘niter’ only after all channels/planes/fields have completed theirminor cycles and exited either due to ‘cycleniter’ or ‘cyclethreshold’.Therefore, the actual number of iterations reported in the loggercan sometimes be larger than the user specified value in ‘niter’.For example, with niter=100, cycleniter=20,nchan=10,threshold=0,a total of 200 iterations will be done in the first set of minor cyclesbefore the total is compared with niter=100 and it exits.Note : Additional global stopping criteria include- no change in peak residual across two major cycles- a 50% or more increase in peak residual across one major cyclegain (double=0.1)- Loop gainFraction of the source flux to subtract out of the residual imagefor the CLEAN algorithm and its variants.A low value (0.2 or less) is recommended when the sky brightnessdistribution is not well represented by the basis functions used bythe chosen deconvolution algorithm. A higher value can be tried whenthere is a good match between the true sky brightness structure andthe basis function shapes. For example, for extended emission,multiscale clean with an appropriate set of scale sizes will toleratea higher loop gain than Clark clean (for example).threshold (double=0.0)- Stopping threshold (number in units of Jy, or string)A global stopping threshold that the peak residual (within clean mask)across all image planes is compared to.threshold = 0.005 : 5mJythreshold = ‘5.0mJy’Note : A ‘cyclethreshold’ is internally computed and used as a major cycletrigger. It is related what fraction of the PSF can be reliablyused during minor cycle updates of the residual image. By defaultthe minor cycle iterations terminate once the peak residual reachesthe first sidelobe level of the brightest source.‘cyclethreshold’ is computed as follows using the settings inparameters ‘cyclefactor’,’minpsffraction’,’maxpsffraction’,’threshold’ :psf_fraction = max_psf_sidelobe_level * ‘cyclefactor’psf_fraction = max(psf_fraction, ‘minpsffraction’);psf_fraction = min(psf_fraction, ‘maxpsffraction’);cyclethreshold = peak_residual * psf_fractioncyclethreshold = max( cyclethreshold, ‘threshold’ )If nsigma is set (>0.0), the N-sigma threshold is calculated (seethe description under nsigma), then cyclethreshold is further modified as,cyclethreshold = max( cyclethreshold, nsgima_threshold )‘cyclethreshold’ is made visible and editable only in theinteractive GUI when tclean is run with interactive=True.nsigma (double=0.0)- Multiplicative factor for rms-based threshold stoppingN-sigma threshold is calculated as nsigma * rms value per image plane determinedfrom a robust statistics. For nsigma > 0.0, in a minor cycle, a maximum of the two values,the N-sigma threshold and cyclethreshold, is used to trigger a major cycle(see also the descreption under ‘threshold’).Set nsigma=0.0 to preserve the previous tclean behavior without this feature.The top level parameter, fastnoise is relevant for the rms noise calculation which is usedto determine the threshold.The parameter ‘nsigma’ may be an int, float, or a double.cycleniter (int=-1)- Maximum number of minor-cycle iterations (per plane) before triggeringa major cycleFor example, for a single plane image, if niter=100 and cycleniter=20,there will be 5 major cycles after the initial one (assuming there is nothreshold based stopping criterion). At each major cycle boundary, ifthe number of iterations left over (to reach niter) is less than cycleniter,it is set to the difference.Note : cycleniter applies per image plane, even if cycleniter x nplanesgives a total number of iterations greater than ‘niter’. This is topreserve consistency across image planes within one set of minorcycle iterations.cyclefactor (double=1.0)- Scaling on PSF sidelobe level to compute the minor-cycle stopping threshold.Please refer to the Note under the documentation for ‘threshold’ thatdiscussed the calculation of ‘cyclethreshold’cyclefactor=1.0 results in a cyclethreshold at the first sidelobe level ofthe brightest source in the residual image before the minor cycle starts.cyclefactor=0.5 allows the minor cycle to go deeper.cyclefactor=2.0 triggers a major cycle sooner.minpsffraction (double=0.05)- PSF fraction that marks the max depth of cleaning in the minor cyclePlease refer to the Note under the documentation for ‘threshold’ thatdiscussed the calculation of ‘cyclethreshold’For example, minpsffraction=0.5 will stop cleaning at half the height ofthe peak residual and trigger a major cycle earlier.maxpsffraction (double=0.8)- PSF fraction that marks the minimum depth of cleaning in the minor cyclePlease refer to the Note under the documentation for ‘threshold’ thatdiscussed the calculation of ‘cyclethreshold’For example, maxpsffraction=0.8 will ensure that at least the top 20percent of the source will be subtracted out in the minor cycle even ifthe first PSF sidelobe is at the 0.9 level (an extreme example), or if thecyclefactor is set too high for anything to get cleaned.interactive (bool=False)- Modify masks and parameters at runtimeinteractive=True will trigger an interactive GUI at every major cycleboundary (after the major cycle and before the minor cycle).Options for runtime parameter modification are :Interactive clean mask : Draw a 1/0 mask (appears as a contour) by hand.If a mask is supplied at the task interface or ifautomasking is invoked, the current mask isdisplayed in the GUI and is available for manualediting.Note : If a mask contour is not visible, pleasecheck the cursor display at the bottom ofGUI to see which parts of the mask imagehave ones and zeros. If the entire mask=1no contours will be visible.Operation buttons : – Stop execution now (restore current model and exit)– Continue on until global stopping criteria are reachedwithout stopping for any more interaction– Continue with minor cycles and return for interactionafter the next major cycle.Iteration control : – max cycleniter : Trigger for the next major cycleThe display begins with[ min( cycleniter, niter - itercount ) ]and can be edited by hand.– iterations left : The display begins with [niter-itercount ]and can be edited to increase ordecrease the total allowed niter.– threshold : Edit global stopping threshold– cyclethreshold : The display begins with theautomatically computed value(see Note in help for ‘threshold’),and can be edited by hand.All edits will be reflected in the log messages that appearonce minor cycles begin.nmajor (int=-1)- The nmajor parameter limits the number of minor and major cycle setsthat tclean executes. It is defined as the number of major cycles after theinitial set of minor cycle iterations. In other words, the count of nmajor doesnot include the initial residual calculation that occurs when calcres=True.A setting of nmajor=-1 implies no limit (default -1).A setting of nmajor=0 implies nothing other than the initial residual calculationA setting of nmajor>0 imples that nmajor sets of minor and major cycles willbe done in addition to the initial residual calculation.If the major cycle limit is reached, stopcode 9 will be returned. Other stoppingcriteria (such as threshold) could cause tclean to stop in fewer than thisnumber of major cycles. If tclean reaches another stopping criteria, firstor at the same time as nmajor, then that stopcode will be returned instead.Note however that major cycle ids in the log messages as well as in the returndictionary do begin with 1 for the initial residual calculation, when it exists.Example 1 : A tclean run with ‘nmajor=5’ and ‘calcres=True’ will iterate for5 major cycles (not counting the initial residual calculation). But, the returndictionary will show ‘nmajordone:6’. If ‘calcres=False’, then the returndictionary will show ‘nmajordone:5’.Example 2 : For both the following cases, there will be a printout in the logs“Running Major Cycle 1” and the return value will include “nmajordone: 1”,however there is a difference in the purpose of the major cycle and thenumber of minor cycles executed:Case 1; nmajor=0, calcres=True: The major cycle done is for the creationof the residual, and no minor cycles are executed.Case 2; nmajor=1, calcres=False: The major cycle is done as part of themajor/minor cycle loop, and 1 minor cycle will be executed.fullsummary (bool=False)- Return dictionary with complete convergence historyfullsummary=True: A full version of the summary dictionary is returned.Keys include ‘iterDone’,’peakRes’,’modelFlux’,’cycleThresh’ that record theconvergence state at the end of each set of minor cycle iterationsseparately for each image plane (i.e. channel/stokes) beingdeconvolved. Additional keys report the convergence state at thestart of minor cycle iterations, stopping criteria that triggered majorcycles, and a processor ID per channel, for parallel cube runs.fullsummary=False (default): A shorten version of the summary dictionary is returnedwith only ‘iterDone’,’peakRes’,’modelFlux’, and ‘cycleThresh’.Detailed information about the return dictionary fields may be foundat CASA Docs > Synthesis Imaging > Iteration Control > Returned Dictionary.Note : With some parallel cube imaging runs that have a large number of channelsand iterations per cube partition in a parallel run, an MPI message passing limit maybe reached due to the size of the return dictionaries being passed around, causingCASA to crash (with fullsummary=True). The limit has been estimated to be reachedonly when nchan_per_chunk x iterdone_per_minorcycleset > 8e+6. The option to setfullsummary=False should be used to guard against this.usemask (string='user')- Type of mask(s) to be used for deconvolutionuser: (default) mask image(s) or user specified region file(s) or string CRTF expression(s)subparameters: mask, pbmaskpb: primary beam masksubparameter: pbmaskExample: usemask=”pb”, pbmask=0.2Construct a mask at the 0.2 pb gain level.(Currently, this option will work only withgridders that produce .pb (i.e. mosaic and awproject)or if an externally produced .pb image exists on disk)auto-multithresh : auto-masking by multiple thresholds for deconvolutionsubparameters : sidelobethreshold, noisethreshold, lownoisethreshold, negativethrehsold, smoothfactor,minbeamfrac, cutthreshold, pbmask, growiterations, dogrowprune, minpercentchange, verboseAdditional top level parameter relevant to auto-multithresh: fastnoiseif pbmask is >0.0, the region outside the specified pb gain level is excluded fromimage statistics in determination of the threshold.Note: By default the intermediate mask generated by automask at each deconvolution cycleis over-written in the next cycle but one can save them by settingthe environment variable, SAVE_ALL_AUTOMASKS=”true”.(e.g. in the CASA prompt, os.environ[‘SAVE_ALL_AUTOMASKS’]=”true” )The saved CASA mask image name will be imagename.mask.autothresh#, where# is the iteration cycle number.mask ({string, stringVec}='')- Mask (a list of image name(s) or region file(s) or region string(s)The name of a CASA image or region file or region string that specifiesa 1/0 mask to be used for deconvolution. Only locations with value 1 willbe considered for the centers of flux components in the minor cycle.If regions specified fall completely outside of the image, tclean will throw an error.Manual mask options/examples :mask=’xxx.mask’ : Use this CASA image named xxx.mask and containingones and zeros as the mask.If the mask is only different in spatial coordinates from what is being madeit will be resampled to the target coordinate system before being used.The mask has to have the same shape in velocity and Stokes planesas the output image. Exceptions are single velocity and/or singleStokes plane masks. They will be expanded to cover all velocity and/orStokes planes of the output cube.[ Note : If an error occurs during image resampling orif the expected mask does not appear, please tryusing tasks ‘imregrid’ or ‘makemask’ to resamplethe mask image onto a CASA image with the targetshape and coordinates and supply it via the ‘mask’parameter. ]mask=’xxx.crtf’ : A text file with region strings and the following on the first line( #CRTFv0 CASA Region Text Format version 0 )This is the format of a file created via the viewer’s regiontool when saved in CASA region file format.mask=’circle[[40pix,40pix],10pix]’ : A CASA region string.mask=[‘xxx.mask’,’xxx.crtf’, ‘circle[[40pix,40pix],10pix]’] : a list of masksNote : Mask images for deconvolution must contain 1 or 0 in each pixel.Such a mask is different from an internal T/F mask that can beheld within each CASA image. These two types of masks are notautomatically interchangeable, so please use the makemask taskto copy between them if you need to construct a 1/0 based maskfrom a T/F one.Note : Work is in progress to generate more flexible masking options andenable more controls.pbmask (double=0.0)- Sub-parameter for usemask: primary beam maskExamples : pbmask=0.0 (default, no pb mask)pbmask=0.2 (construct a mask at the 0.2 pb gain level)sidelobethreshold (double=3.0)- Sub-parameter for “auto-multithresh”: mask threshold based on sidelobe levels: sidelobethreshold * max_sidelobe_level * peak residualnoisethreshold (double=5.0)- Sub-parameter for “auto-multithresh”: mask threshold based on the noise level: noisethreshold * rms + location (=median)The rms is calculated from MAD with rms = 1.4826*MAD.lownoisethreshold (double=1.5)- Sub-parameter for “auto-multithresh”: mask threshold to grow previously masked regions via binary dilation: lownoisethreshold * rms in residual image + location (=median)The rms is calculated from MAD with rms = 1.4826*MAD.negativethreshold (double=0.0)- Sub-parameter for “auto-multithresh”: mask threshold for negative features: -1.0* negativethreshold * rms + location(=median)The rms is calculated from MAD with rms = 1.4826*MAD.smoothfactor (double=1.0)- Sub-parameter for “auto-multithresh”: smoothing factor in a unit of the beamminbeamfrac (double=0.3)- Sub-parameter for “auto-multithresh”: minimum beam fraction in size to prune masks smaller than mimbeamfrac * beam<=0.0 : No pruningcutthreshold (double=0.01)- Sub-parameter for “auto-multithresh”: threshold to cut the smoothed mask to create a final mask: cutthreshold * peak of the smoothed maskgrowiterations (int=75)- Sub-parameter for “auto-multithresh”: Maximum number of iterations to perform using binary dilation for growing the maskdogrowprune (bool=True)- Experimental sub-parameter for “auto-multithresh”: Do pruning on the grow maskminpercentchange (double=-1.0)- If the change in the mask size in a particular channel is less than minpercentchange, stop masking that channel in subsequent cycles. This check is only applied when noise based threshold is used and when the previous clean major cycle had a cyclethreshold value equal to the clean threshold. Values equal to -1.0 (or any value less than 0.0) will turn off this check (the default). Automask will still stop masking if the current channel mask is an empty mask and the noise threshold was used to determine the mask.verbose (bool=False)- If it is set to True, the summary of automasking at the end of each automasking processis printed in the logger. Following information per channel will be listed in the summary.chan: channel numbermasking?: F - stop updating automask for the subsequent iteration cyclesRMS: robust rms noisepeak: peak in residual imagethresh_type: type of threshold used (noise or sidelobe)thresh_value: the value of threshold usedN_reg: number of the automask regionsN_pruned: number of the automask regions removed by pruningN_grow: number of the grow mask regionsN_grow_pruned: number of the grow mask regions removed by pruningN_neg_pix: number of pixels for negative mask regionsNote that for a large cube, extra logging may slow down the process.fastnoise (bool=True)- Only relevant when automask (user=’multi-autothresh’) and/or n-sigma stopping threshold (nsigma>0.0) are/is used. If it is set to True, a simpler but faster noise calucation is used.In this case, the threshold values are determined based on classic statistics (using allunmasked pixels for the calculations).If it is set to False, the new noise calculationmethod is used based on pre-existing mask.Case 1: no exiting maskCalculate image statistics using Chauvenet algorithmCase 2: there is an existing maskCalculate image statistics by classical method on the regionoutside the mask and inside the primary beam mask.In all cases above RMS noise is calculated from MAD.restart (bool=True)- Restart using existing images (and start from an existing model image)or automatically increment the image name and make a new image set.True : Re-use existing images. If imagename.model exists the subsequentrun will start from this model (i.e. predicting it using current griddersettings and starting from the residual image). Care must be takenwhen combining this option with startmodel. Currently, only one orthe other can be used.startmodel=’’, imagename.model exists :- Start from imagename.modelstartmodel=’xxx’, imagename.model does not exist :- Start from startmodelstartmodel=’xxx’, imagename.model exists :- Exit with an error message requesting the user to pickonly one model. This situation can arise when doing onerun with startmodel=’xxx’ to produce an outputimagename.model that includes the content of startmodel,and wanting to restart a second run to continue deconvolution.Startmodel should be set to ‘’ before continuing.If any change in the shape or coordinate system of the image isdesired during the restart, please change the image name anduse the startmodel (and mask) parameter(s) so that the old model(and mask) can be regridded to the new coordinate system before starting.False : A convenience feature to increment imagename with ‘_1’, ‘_2’,etc as suffixes so that all runs of tclean are fresh starts (withouthaving to change the imagename parameter or delete images).This mode will search the current directory for all existingimagename extensions, pick the maximum, and adds 1.For imagename=’try’ it will make try.psf, try_2.psf, try_3.psf, etc.This also works if you specify a directory name in the path :imagename=’outdir/try’. If ‘./outdir’ does not exist, it will create it.Then it will search for existing filenames inside that directory.If outlier fields are specified, the incrementing happens for eachof them (since each has its own ‘imagename’). The counters aresynchronized across imagefields, to make it easier to match up setsof output images. It adds 1 to the ‘max id’ from all outlier nameson disk. So, if you do two runs with only the main field(imagename=’try’), and in the third run you add an outlier withimagename=’outtry’, you will get the following image namesfor the third run : ‘try_3’ and ‘outtry_3’ even though‘outry’ and ‘outtry_2’ have not been used.savemodel (string='none')- Options to save model visibilities (none, virtual, modelcolumn)Often, model visibilities must be created and saved in the MSto be later used for self-calibration (or to just plot and view them).none : Do not save any model visibilities in the MS. The MS is openedin readonly mode.Model visibilities can be predicted in a separate step byrestarting tclean with niter=0,savemodel=virtual or modelcolumnand not changing any image names so that it finds the .model ondisk (or by changing imagename and setting startmodel to theoriginal imagename).virtual : In the last major cycle, save the image model and state of thegridder used during imaging within the SOURCE subtable of theMS. Images required for de-gridding will also be stored internally.All future references to model visibilities will activate the(de)gridder to compute them on-the-fly. This mode is usefulwhen the dataset is large enough that an additional model datacolumn on disk may be too much extra disk I/O, when thegridder is simple enough that on-the-fly recomputing of themodel visibilities is quicker than disk I/O.For e.g. that gridder=’awproject’ does not support virtual model.modelcolumn : In the last major cycle, save predicted model visibilitiesin the MODEL_DATA column of the MS. This mode is useful whenthe de-gridding cost to produce the model visibilities is higherthan the I/O required to read the model visibilities from disk.This mode is currently required for gridder=’awproject’.This mode is also required for the ability to later pull outmodel visibilities from the MS into a python array for customprocessing.Note 1 : The imagename.model image on disk will always be constructedif the minor cycle runs. This savemodel parameter applies only tomodel visibilities created by de-gridding the model image.Note 2 : It is possible for an MS to have both a virtual modelas well as a model_data column, but under normal operation,the last used mode will get triggered. Use the delmod task toclear out existing models from an MS if confusion arises.Note 3: when parallel=True, use savemodel=’none’; Other options are not yet readyfor use in parallel. If model visibilities need to be saved (virtual or modelcolumn):please run tclean in serial mode with niter=0; after the parallel runcalcres (bool=True)- Calculate initial residual imageThis parameter controls what the first major cycle does.calcres=False with niter greater than 0 will assume thata .residual image already exists and that the minor cycle canbegin without recomputing it.calcres=False with niter=0 implies that only the PSF will be madeand no data will be gridded.calcres=True requires that calcpsf=True or that the .psf and .sumwtimages already exist on disk (for normalization purposes).Usage example : For large runs (or a pipeline scripts) it may beuseful to first run tclean with niter=0 to createan initial .residual to look at and perhaps makea custom mask for. Imaging can be resumedwithout recomputing it.calcpsf (bool=True)- Calculate PSFThis parameter controls what the first major cycle does.calcpsf=False will assume that a .psf image already existsand that the minor cycle can begin without recomputing it.psfcutoff (double=0.35)- When the .psf image is created a 2 dimensional Gaussian is fit to the main lobe of the PSF.Which pixels in the PSF are fitted is determined by psfcutoff.The default value of psfcutoff is 0.35 and can varied from 0.01 to 0.99.Fitting algorithm:- A region of 41 x 41 pixels around the peak of the PSF is compared against the psfcutoff.Sidelobes are ignored by radially searching from the PSF peak.- Calculate the bottom left corner (blc) and top right corner (trc) from the points. Expand blc and trc with a number of pixels (5).- Create a new sub-matrix from blc and trc.- Interpolate matrix to a target number of points (3001) using CUBIC spline.- All the non-sidelobe points, in the interpolated matrix, that are above the psfcutoff are used to fit a Gaussian.A Levenberg-Marquardt algorithm is used.- If the fitting fails the algorithm is repeated with the psfcutoff decreased (psfcutoff=psfcutoff/1.5).A message in the log will apear if the fitting fails along with the new value of psfcutoff.This will be done up to 50 times if fitting fails.This Gaussian beam is defined by a major axis, minor axis, and position angle.During the restoration process, this Gaussian beam is used as the Clean beam.Varying psfcutoff might be useful for producing a better fit for highly non-Gaussian PSFs, however, the resulting fits should be carefully checked.This parameter should rarely be changed.(This is not the support size for clark clean.)parallel (bool=False)- Run major cycles in parallel (this feature is experimental)Parallel tclean will run only if casa has already been started using mpirun.Please refer to HPC documentation for details on how to start this on your system.Example : mpirun -n 3 -xterm 0 which casaContinuum Imaging :- Data are partitioned (in time) into NProc pieces- Gridding/iFT is done separately per partition- Images (and weights) are gathered and then normalized- One non-parallel minor cycle is run- Model image is scattered to all processes- Major cycle is done in parallel per partitionCube Imaging :- Data and Image coordinates are partitioned (in freq) into NProc pieces- Each partition is processed independently (major and minor cycles)- All processes are synchronized at major cycle boundaries for convergence checks- At the end, cubes from all partitions are concatenated along the spectral axisNote 1 : Iteration control for cube imaging is independent per partition.- There is currently no communication between them to synchronizeinformation such as peak residual and cyclethreshold. Therefore,different chunks may trigger major cycles at different levels.(Proper synchronization of iteration control is work in progress.)